Problema 493.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid)

Hallar el área del único triángulo escaleno (módulo rotaciones) formado desde los tres vértices de un heptágono regular, teniendo los ángulos ,, respectivamente, inscrito en una circunferencia de radio R.

Resolución: (Vicente Vicario García)

            Determinaremos el área del triángulo pedido de dos formas diferentes, comprobando, obviamente, la coincidencia de los resultados.

Método 1: Sea el heptágono regular ABCDEFG inscrito en una circunferencia de radio R, y sea L el lado del mismo. Desde el vértice A trazamos las diagonales AC, AD, AE y AF obteniendo una triangulación del heptágono en cinco triángulos. Dos de ellos, los triángulos ABC y AFG son congruentes e isósceles; otros dos, los triángulos ACD y AEF son triángulos congruentes y del tipo pedido en el enunciado del problema, y el triángulo ADE es isósceles. Descompongamos pues, el área del heptágono regular inscrito como suma de áreas de estos cinco triángulos y de aquí, obtengamos el área pedida, determinando previamente el área de los demás triángulos.

            El área del heptágono regular inscrito en la circunferencia de radio R, teniendo en cuenta que , viene dado por

           

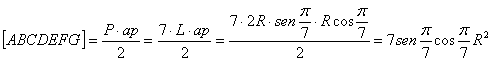
            Por otra parte, el área del triángulo isósceles ABC, teniendo en cuenta que el ángulo interior del heptágono regular es , viene dado por

           

ya que evidentemente , por ser estos ángulos suplementarios.

            El área del triángulo isósceles ADE viene dado, teniendo en cuenta que  es la mitad del ángulo central, y consideraciones trigonométricas elementales, viene dado por

           

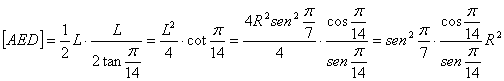
            Planteando ahora la igualdad entre áreas tenemos que

                                  

lo que nos lleva a las expresiones siguientes

             

donde hemos tenido en cuenta identidades trigonométricas elementales y fórmulas de transformación de productos en sumas.

            Si queremos expresar el cociente del área de este triángulo ACD de ángulos ,, con respecto al área del heptágono regular, podemos escribir

           

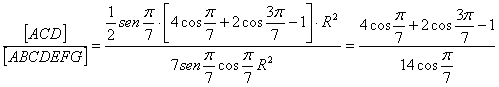
Método 2: Aquí haremos uso de los números complejos sobre la circunferencia unidad y de la expresión del área de un triángulo en el espacio en función del producto vectorial de dos de los vectores que conforman sus lados.

            Sean ABCDEFG los vértices consecutivos de un heptágono regular inscrito en una circunferencia de radio R. Sin pérdida de generalidad, supondremos inicialmente el radio unidad. Los números complejos asociados a los vértices del heptágono serán entonces

                   .

            Consideremos ahora el triángulo ACD cuyos vértices son conocidos y pasemos los números complejos de la forma euleriana a su forma binómico. Es entonces claro que por geometría analítica elemental, el área de dicho triángulo viene dado por

           

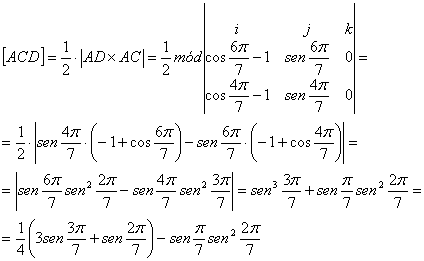
donde hemos hecho uso de las fórmulas del ángulo mitad y del ángulo triple  y de trigonometría elemental. Finalmente, podemos comprobar la coincidencia de los resultados de los dos métodos. Para ello, podemos observar que

           

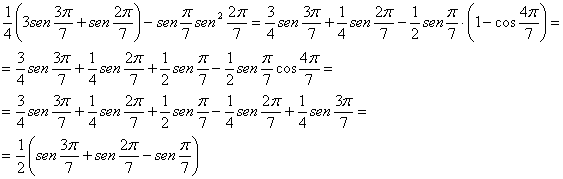
donde hemos utilizado las fórmulas de transformación de productos en sumas y trigonometría elemental. Así pues, el área del triángulo pedido será

                                   

que, evidentemente, coincide con el resultado aplicando el método anterior.

---oooOooo---