Para el aula
Problema 494
Construir un triángulo ABC del que conocemos los vértices A’ B’ C’ de los triángulos equiláteros BCA’, CAB’ , ABC’ hacia el exterior.
Yaglom , IM (1962) Geometric
transformations I M.A.A. Yagloom I. (1973): Geometric Transformations I. The
Mathematical Association of
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
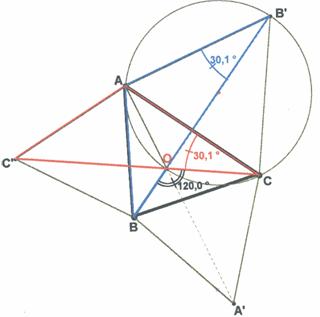 Partimos de la solución del problema, o sea, construimos el triángulo
ABC y realizamos los triángulos equiláteros BCA’, CAB’, ABC’ hacia el exterior.
Partimos de la solución del problema, o sea, construimos el triángulo
ABC y realizamos los triángulos equiláteros BCA’, CAB’, ABC’ hacia el exterior.
Observemos los triángulos AC’C y ABB’; si hacemos un giro de 60º con centro en el vértice A de los segmentos AC’ y AC se transforman en los segmentos AB y AB’ luego los triángulos AC’C y ABB’ son iguales y al transformarse por el giro de 60º C’C en BB’ podemos deducir:
- Los segmentos AA’, BB’ y CC’ son iguales.
- Los segmentos AA’, BB’ y CC forman entre sí 60º.
Observemos el punto de corte O de los segmentos C’C y BB’. El punto O estará en un arco capaz de 120º del segmento BC (el suplementario de 60º). Por la misma razón el punto O estará en los arcos capaces de 120º de los segmentos AB y CA. Como solo hay una solución podemos deducir que las rectas AA’, BB’ y CC’ (bien partiendo de A, B y C o de A’, B’ y C’) además de formar 60º entre sí se cortan en un único punto O. Luego partiendo del triángulo A’B’C’ se puede dibujar el punto O mediante la intersección de dos arcos capaces de 120º de dos de los lados
Observemos el cuadrilátero AOCB’. Los ángulos ACO y AB’O son iguales puesto que pertenecen a triángulos iguales y como tienen AO común pueden ser ángulos inscritos en una circunferencia cuya cuerda común sea AO por lo tanto el cuadrilátero AOCB’ es inscriptible. Aplicando el teorema de Ptolomeo “Si un cuadrilátero puede ser inscrito en un círculo, la suma de los productos de las dos parejas de lados opuestos es igual al producto de las diagonales”:
(AB’)(OC)+(OA)(CB’) = (AC) (OB’), Por
la misma razón OC+OB=OA’ y OB+OA=OC’
poniendo OA en función de los datos conocidos sale OA = [(OB’) + (OC’) - (OA’)] / 2
OA+OA’ = AA’ = BB’ = CC’. Luego en las semirrectas A’O, B’O y C’O llevando la magnitud AA’ obtenida por el teorema de Ptolomeo resuelve el problema