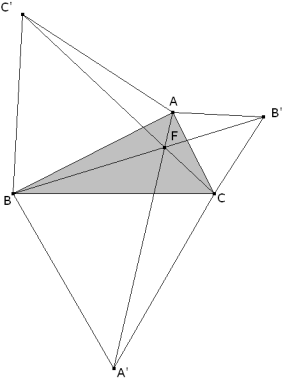
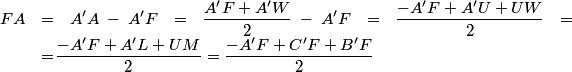Problema 494. Construir un triángulo ABC del que conocemos los vértices A’ B’ C’ de los triángulos equiláteros BCA’, CAB’, ABC’ hacia el exterior. Yaglom , IM (1962) Geometric transformations I M.A.A. Yagloom I. (1973): Geometric Transformations I. The Mathematical Association of America . (traducido del ruso al ingles por Allen Shields). (p. 12) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de enero de 2009) |
|
Presentaremos dos soluciones:
|
|
Primera solución |
|
|
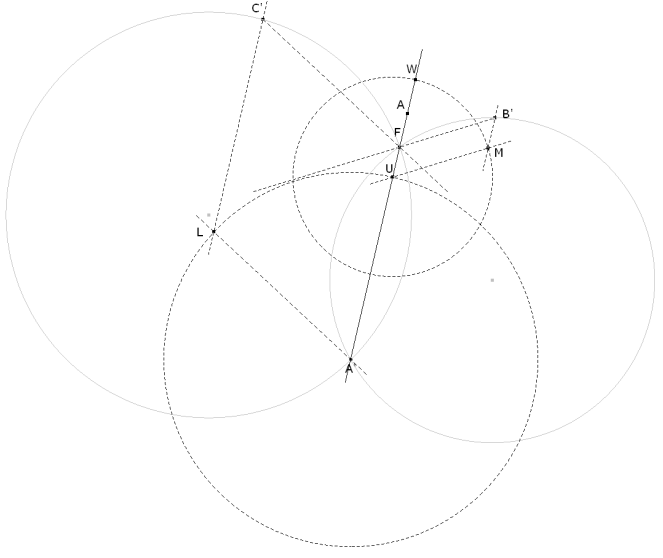
Supongamos el problema resuelto y estudiemos la figura.
Es sabido en la geometría del triángulo que las rectas que unen los vértices del triángulo dado y los vértices opuestos de los triángulos equiláteros sobre la base opuesta concurren en un punto denominado punto de FERMAT o llamado también punto de TORRICELLI. Recordemos que éste es también la solución al problema de encontrar el punto cuya suma de distancias a los vértices del triángulo es mínima. Demostremos esa concurrencia:
Supongamos que BB' y CC' se cortan en un punto F; deberemos demostrar que A, F, y A' son colineales. Los triángulos C'AC y BAB' son congruentes, ya que BAB' no es más que la rotación de 60° en torno a A del triángulo C'AC. De lo que se desprende que:
Por los arcos que abarca el segmento AB, los puntos AC'BF son concíclicos. Por un razonamiento análogo, también son concíclicos los puntos AFCB'. Podemos pues asegurar que:
Pero entonces:
lo que nos indica que los puntos BA'CF también son concíclicos. Tenemos así que:
y como
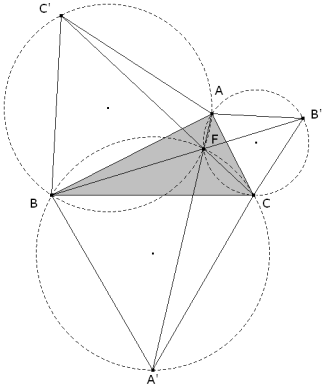
deducimos que: AFA' están en línea recta. Demostrado lo anterior podemos trazar el punto F
ya que al ser
F estará en la intersección de los tres arcos capaces de 120° de los segmentos A'B', B'C' y C'A'.
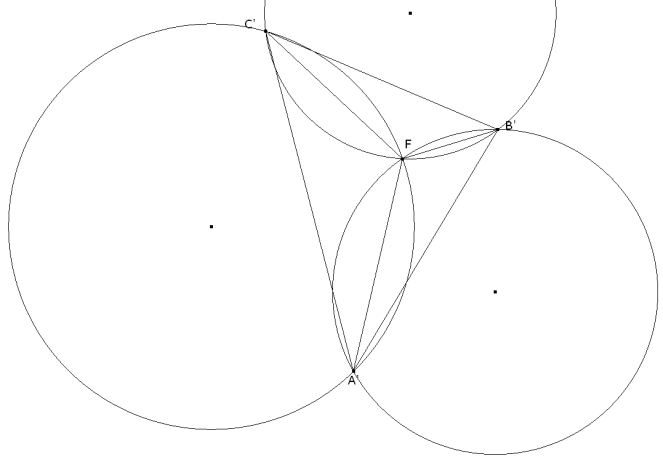
Retomaando la figura 2, donde hemos visto que los puntos AFCB' son concíclicos, trazamos las perpendiculares respectivas a AF y a CF en A y en C, que se cortan en B"; tenemos entonces que
por lo que los puntos AFCB" también son concíclicos y en consecuencia B" está sobre el mismo círculo que AFCB'; pero el ángulo capaz del segmento CA es de 60° con lo que también será
y un razonamiento análogo nos lleva a que si trazásemos la perpendicular correspondiente a BF en B, que corta a las perpendiculares anteriores en A" y C", obtenemos
De ello se deduce que: ¡¡ El triángulo “anti-pedal” del punto F es equilátero !! De este resultado deducimos la solución del problema de mínimos enunciado al principio: El punto de Fermat F es el punto cuya suma de distancias a los vértices es mínima. Este mínimo es igual a la altura del triángulo equilátero A"B"C" “anti-pedal” de F. En efecto, hemos visto que A"B"C" es equilátero. Las longitudes AF, BF, y CF son las distancias de F a los lados de este triángulo. Ahroa bien, para todos los puntos situados en el interior de un triángulo equilátero, la suma de distancias a los lados es constante e igual a la altura del triángulo, como para cualquier otro punto P las longitudes AP, BP y CP son oblícuas cuya suma es más grande que la altura del triángulo “anti-pedal”. Pero como el ángulo ∠FAB" es recto, FB" es el diámetro del círculo FAB'B"C y el ángulo ∠FB'B" también es recto; luego, ya que BFB' es perpendicular, simultáneamente, a B'B" y a C"A", es igual a la perpendicular BB' desde B" a C"A" y por lo tanto: Los segmento AA', BB' y CC' son iguales entre sí e iguales a la altura del triángulo equilátero “anti-pedal” del punto F De ello obtenemos que:
Y a su vez:
De ellos obtenemos:
y de aquí los puntos A, B, y C.
De manera análoga completamos los puntos B y C. Primera solución dinámica |
|
Segunda solución |
|
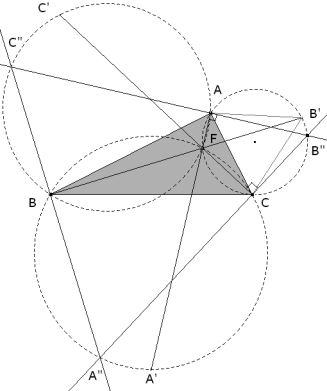
Se puede construir un triángulo ABC, conociendo los vértices A', B' y C' de los triángulos equiláteros construidos sobre los lados. E.LEMOINE Construimos sobre A'B'C' los triángulos equiláteros A'B'C", A'C'B", B'C'A"; los puntos medios de A'A", B'B" y C'C" son los vértices A, B, y C del triángulo buscado. KIEPERT Segunda solución dinámica |