Problema 494

Construïu un triangle  del qual coneguem els vèrtexs A’, B’, C’ dels triangles

equilàters , ,  exteriors al triangle .

Solució Ricard Peiró i Estruch.

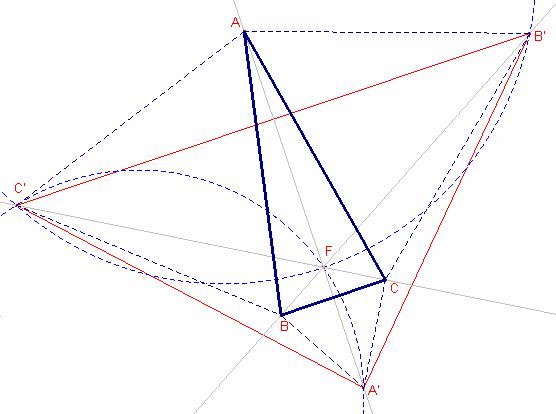
En aquesta construcció, les rectes AA’, BB’, CC’ s’intersecten en el punt de Fermat F que acompleix que:

a) F és el punt que la suma de les distàncies de F als vèrtex del triangle és mínima.

b) .

c) .

d) .

El quadrilàter  és inscriptible ja que els angles oposats F, C’ són suplementaris.

Aplicant el teorema de Tolomeu:

.

. Simplificant:

                                           (1)

Anàlogament:

                                            (2)

                                           (3)

Resolent el sistema format per les expressions (1) (2) (3):

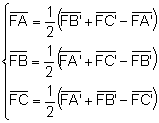
Mètode de construcció:

a) Determinar els arcs capaços de 120º sobre els costats .

b) La intersecció dels arcs és F el punt de Fermat.

c) Calcular .

d) Dibuixar les rectes FA’, FB’, FC’.

e) Dibuixar sobre la recta FA’ el segment

f) Dibuixar sobre la recta FB’ el segment

g) Dibuixar sobre la recta FC’ el segment

Amb Cabri:

Figurabarroso494.fig

Applet created on 18/01/09 by Ricard Peiró with CabriJava