Problema 494
Construir un triángulo ABC del que conocemos los vértices A’ B’ C’ de los triángulos equiláteros BCA’, CAB’ , ABC’ hacia el exterior.
Yaglom , IM (1962) Geometric transformations
I M.A.A. Yagloom I. (1973): Geometric
Transformations I. The Mathematical Association of
Solución Ricard Peiró i Estruch.
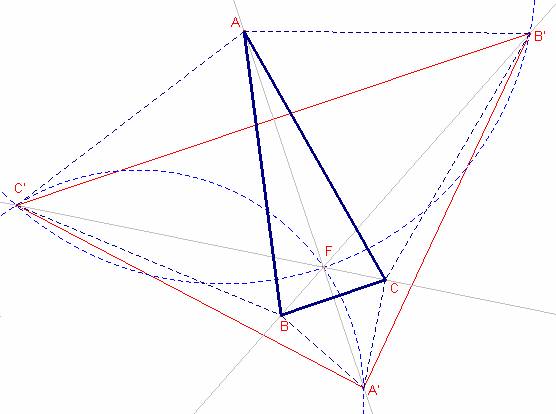
En esta construcción, las rectas AA’, BB’, CC’ se intersectan en el punto de Fermat F que cumple:
a) F es el punto que la suma de las distancias de F a los vértices del triángulo es mínima.
b) 
.
c) 
.
d) 
.
El cuadrilátero 
es inscriptible ya que los ángulos opuestos F, C’ son suplementarios.
Aplicando el teorema de Tolomeo:
.
. Simplificando:
(1)
Análogamente:
(2)
(3)
Resolviendo el sistema formado por las expresiones (1) (2) (3):
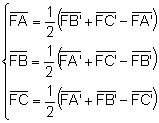
Métodoe de construcción:
a) Determinar los arcos capaces de 120º sobre los
lados 
.
b) La intersección de los arcos es F el punto de Fermat.
c) Calcular 
.
d) Dibujar les rectas FA’, FB’, FC’.
e) Dibujar sobre la recta FA’ el segmento 
f) Dibujar sobre la recta FB’ el segmento 
g) Dibujar sobre la recta FC’ el segmento 
Con Cabri:
Figura barroso494.fig
Applet created on 18/01/09 by Ricard Peiró with CabriJava