Problema 495.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva).

Sea un triángulo ABC, su área, las longitudes de sus medianas y las longitudes de sus bisectrices interiores. Demostrar las siguientes desigualdades:

(a)

(b)

Vicario, V. (2008): Comunicación personal

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo junto con las bien conocidas expresiones de las longitudes de las medianas y de las bisectrices interiores de un triángulo, además de la expresión clásica del coseno del ángulo mitad

, ,

, , ,

(a) Para cualquier mediana tenemos claramente la siguiente desigualdad

y aplicando también la desigualdad entre las medias aritmética y geométrica, entonces

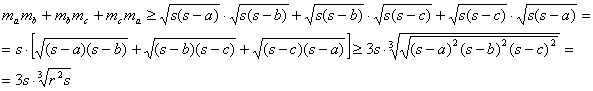
Por otra parte, como , aplicando la desigualdad entre las medias aritmética y geométrica

[*]

con lo que

y la última desigualdad ya estaba demostrada en el lema. Eso concluye la demostración.

(b) En este caso demostraremos un resultado intermedio que necesitaremos posteriormente. Sea el triángulo ABC y sea D el pie de la mediana . Sea el ángulo formado por la mediana y la bisectriz interior . Sea el punto A´ tal que ABA´C resulta ser un paralelogram0. Entonces tenemos que , , , , y .

Aplicando el teorema de los senos al triángulo AA´C tenemos que

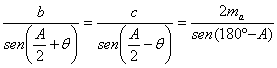
de donde se deduce fácilmente que

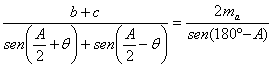
y en consecuencia

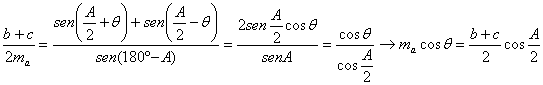
y puesto que , tenemos que

Finalmente, a partir de [*] y la última desigualdad, tenemos que

lo que concluye la demostración.