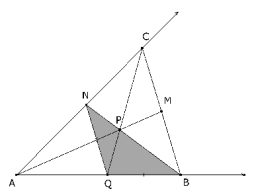
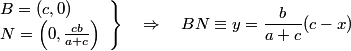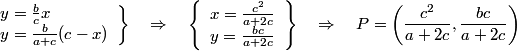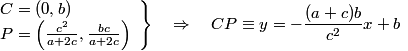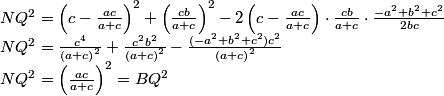Problema 496 J43.- En un triángulo ABC, la mediana AM interseca a la bisectriz interior BN en P. Sea Q el punto de intersección de CP y AB. Demostrar que el triángulo BNQ es isósceles.
Propuesto por Dr. Titu Andreescu, University of Texas at Dallas http://reflections.awesomemath.org/2007_2/problems.pdf Mathematical Reflections (2007, Issue 2) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de febrero de 2009 |
|
|
Vamos a presentar dos soluciones;
|
|
Primera solución |
|
(Este tipo de solución se puede encontrar en las soluciones de la propia revista Reflections) Trazamos la figura
Si examinamos la figura trazada, parece que QN y BC son paralelos; si fuera así, podríamos hallar todos los ángulos y con ellos contestar a la cuestión pedida. Por el enunciado sabemos que El teorema de CEVA nos dice que los segmentos que las tres cevianas concurrentes forman en los lados del triángulo cumplen:
pero com M es el punto medio de BC
que nos indica que los triángulos AQN y ABC son homotéticos y por lo tanto con los mismos ángulos y de aquí
Como en el triángulo BCN
y sobre CA
obtenemos que
pero el triángulo BNQ es isósceles por tener dos ángulos iguales. |
|
Segunda solución |
|
|
Con la misma figura
Si tomamos como sistema de referencia el origen en A y ejes AB y AC las coordenadas de los puntos son
donde a, b, c son (como de costumbre) los lados del triángulo y n es un valor que vamos a determinar gracias al teorema de las bisectrices.
Vamos a determinar P como intersección de AM con BN. Ecuación de la recta AM
Ecuación de la recta BN
La intersección P es
Determinamos la recta CP
Esta última recta encuentra a AB (y = 0) en Q
y de aquí obtenemos BQ
Para NQ a partir de obtenemos
Y por tanto BQ = NQ, lo que nos indica que el triángulo BNQ es isósceles. |
, que M es el punto medio de BC y AM, BN, y CQ concurren en P.
.
y 
