Problema 496

Problema 496 J43.- En un triángulo , la mediana interseca a la bisectriz interior en P. Sea Q el punto de intersección de y . Demostrar que el triángulo es isósceles.

Propuesto por Dr. Titu Andreescu, University of Texas at Dallas

http://reflections.awesomemath.org/2007_2/problems.pdf

Mathematical Reflections (2007, Issue 2)

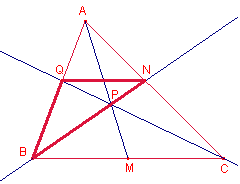
Solución Ricard Peiró i Estruch:

Sea M el punto medio del lado . Sea .

El punto P es la intersección de tres cevianas . Aplicando el teorema de Ceva:

(1)

Aplicando la propiedad de la bisectriz: (2)

Substituyendo la expresión (2) en la expresión (1) y simplificando:

(3)

Aplicando el teorema de los senos al triángulo :

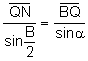(4)

Aplicando el teorema de los senos al triángulo :

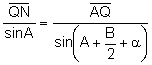(5)

Dividiendo las expresiones (4) y (5): 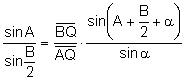(6)

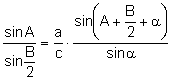(7)

Aplicando el teorema de los senos al triángulo :

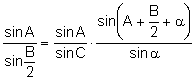(8)

(9)

Transformando en sumas:

(10)

.

Entonces, por tanto el triángulo es isósceles.