Problema
496.-
J43.- En un triángulo ABC, la mediana
interseca a la bisectriz interior BN en P.
Sea Q el punto de intersección de CP y
AB.
Demostrar que el triángulo BNQ es
isósceles.
Propuesto por Dr. Titu
Andreescu,
http://reflections.awesomemath.org/2007_2/problems.pdf.
Mathematical Reflections (2007, Issue 2).
Solución

Para
demostrar que el triángulo BNQ es
isósceles bastará con probar que el lado QN
es paralelo a BC, pues al ser BN la bisectriz el ángulo <QNB es
igual al ángulo <NBC =<QBN.
Esto
es consecuencia de una propiedad de los puntos de la mediana:
Dado un
triángulo ABC, tracemos la recta s
que contiene a la mediana AM. Tomemos P, un punto cualquiera de s.
Tracemos las rectas BP y CP, que cortarán a AC y a AB, o sus prolongaciones, en
Q y T. Demostrar que TQ es paralela a BC.
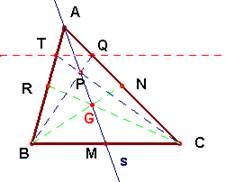
En la figura observamos que la proyección desde B
sobre AC de la cuaterna alineada A,G,P,M
nos da la cuaterna A,N,Q,C. Proyectando desde C la misma cuaterna
ahora sobre el lado AB la cuaterna A,R,T,B, donde G es el
baricentro, CR y BN las medianas que salen de C y B
respectivamente. Como la razón doble de 4 puntos alineados es un invariante
proyectivo, de ahí se siguen las igualdades de razones dobles (ANQC) = (ARTB)
=(AGPM).
(ANQC) = ![]() =
= ![]() = (ARTB) =
= (ARTB) = 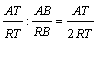 .
.
Se tiene pues, ![]() · Deducimos que los
triángulos ATQ y ABC son semejantes, pues tiene un ángulo común
(el BAC) y los lados que lo forman son proporcionales; por consiguiente
el lado restante TQ ha de ser paralelo a BC.
· Deducimos que los
triángulos ATQ y ABC son semejantes, pues tiene un ángulo común
(el BAC) y los lados que lo forman son proporcionales; por consiguiente
el lado restante TQ ha de ser paralelo a BC.
Y con esto concluye el problema.