Problema 496.- En un triángulo ABC la mediana AM interseca a la bisectriz interior BN en P. Sea Q el punto de intersección de CP y AB. Demostrar que el triángulo BNQ es isosceles.

(Propuesto por Dr. Titu Andreescu, University of Texas at Dallas, MMRR, 2007-2)

Resolución: (Vicente Vicario García, Huelva, Spain)

Utilizaremos la notación habitual en la geometría del triángulo. Por el teorema de Ceva, tenemos que:

Empleando ahora las relaciones clásicas para las longitudes de los segmentos que dejan las bisectrices interiores de un triángulo (deducibles a partir del teorema de la bisectriz interior), tenemos que

, , ,

y sustituyendo en la primera relación

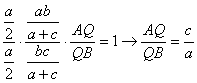[1]

Por otra parte,,. Y usando [1] entonces

[2]

Por el teorema de Stewart podemos deducir fácilmente la expresión de cualquier bisectriz interior en función de los lados del triángulo, y tenemos

y por el teorema de los cosenos aplicado al triángulo BQN, entonces

Usando ahora la identidad trigonométrica clásica (en la que empleamos el signo positivo puesto que ) y el teorema de los cosenos aplicado al triángulo ABC (), tenemos

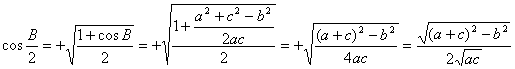
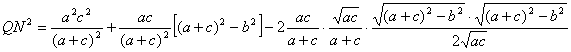
y entonces, por [2], se deduce que el triángulo BNQ es isósceles.

---oooOooo---