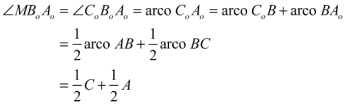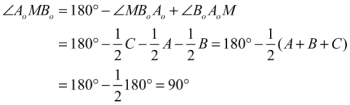Problema 497. Sea ABC un triángulo y G su circunferencia circunscrita. Sean Co el punto medio del arco AB, Bo el punto medio del arco CA y Ao el punto medio del arco BC. Demuestra que el incentro del triángulo ABC es el ortocentro del AoBoCo

XI Olimpiada de Yucatán. 1997

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). 17 de febrero de 2009

Solución

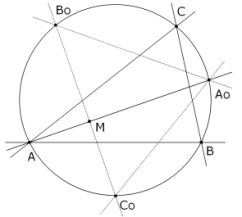
Trazamos la figura de acuerdo con el enunciado.

figura 1

Como el incentro está en la intersección de las bisectrices, y wl ortocentro en la intersección de las alturas, bastará demostrar que la bisectriz AAo del triángulo ABC es una altura del triángulo AoBoCo. Para ello demostraremos que AAo es perpendicular a BoAo.

Damos por sabido que la bisectriz por el vértice de un triángulo pasa por el punto medio del arco opuesto a ese vértice en el círculo circunscrito.

Suponemos que AAo y BoCo se cortan en el punto M.

Para ello relacionamos los arcos en el círculo circunscrito con sus ángulos capaces y para el ángulo BoAoM obtenemos

.

Para el ángulo MBoAo

Y en el triángulo BoAoM

Por lo tanto la bisectriz AAo es perpendicular aº la base BoCo y pasa por Ao; por tanto es una altura de AoBoCo. Análogamente ocurre con BBo y Cco.

Por lo tanto el punto de concurrencia de AAo, BBo, CCo
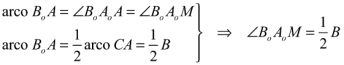es el incentro de ABC y el ortocentro de AoBoCo.