Problema 497

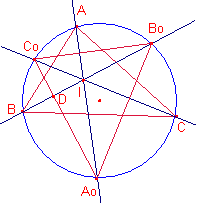Sea el triángulo y G la circunferencia circunscrita. Sean el punto medio del arco , punto medio del arco y punto medio del arco . Probar que el incentro del triángulo es el ortocentro del triángulo .

Solución de Ricard Peiró:

Sea D la intersección de i .

es la bisectriz del vértice B ya que .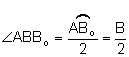

Análogamente , son bisectrices del triángulo .

.

.

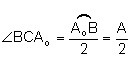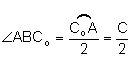Entonces, .

Entonces, .

Entonces, la recta es altura del triángulo .

Análogamente son rectas alturas de .

Entonces, el incentro del triángulo es el ortocentro del triángulo .