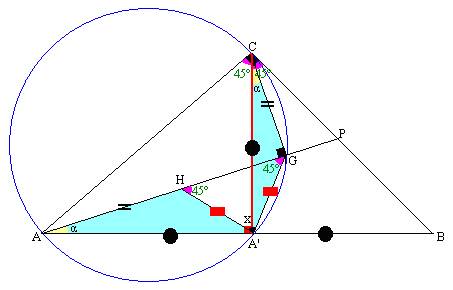
Problema 498

B. 3991. El triángulo isósceles ABC tiene un ángulo recto en C. Sea P un punto arbitrario del lado BC y sea G la proyección ortogonal del punto C sobre AP. Sea H el punto de AP tal que AH =CG. Sea A’ el punto medio de AB. Hallar el valor del ángulo GA’H

Komal marzo 2007

Solución de Julio A. Miranda Ubaldo,  profesor del I.E.P "San Francisco de Asís" de Huaral, de Perú

Grafica del problema Nº 498

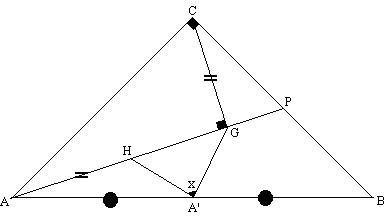
Solución del problema:

*Siendo el triángulo ACB rectángulo e isósceles : CA’ es mediana, altura y bisectriz , por lo tanto AA’ = A’B = CA’ además m< ACA’ = m < BCA’ = 45º.

*El cuadrilátero ACGA’ es inscriptible , entonces m< GAA’ = m < GCA’ = α. y

m< ACA’ = m < AGA’ = 45º.

*Notemos que el triángulo AHA’ es congruente con el triángulo A’CG (criterio LAL)

Entonces HA’ = GA’.

*De la figura el triángulo HA’G es isósceles por lo tanto m< GHA’ = m < HGA’ = 45º

Finalmente m< GA’H = 90º