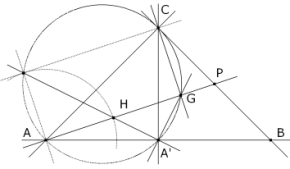
Problema 498. B. 3991. El triángulo isósceles ABC tiene un ángulo recto en C. Sea P un punto arbitrario del lado BC y sea G la proyección ortogonal del punto C sobre AP. Sea H el punto de AP tal que AH =CG. Sea A’ el punto medio de AB. Hallar el valor del ángulo GA’H

Komal marzo 2007

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 de febrero de 2009

Solución

Trazamos la figura de acuerdo con el enunciado.

figura 1

Al trazar la figura, no hemos recurrido a ningún tipo de función trascendental, y por el PRINCIPIO DE CORRESPONDENCIA ANARMÓNICA DE CHASLES, podemos asegurar que la relación entre las rectas del haz con vértice en A'

A'G → A'H

es algebraica y por lo tanto la transformación que a la recta A'G hace corresponder la recta A'H es una homografía.

Identífiquemos dicha homografía mediante tres pares sencillos de rectas correspondientes.

P ≡ C

figura 2

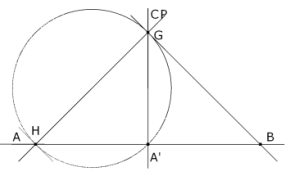
Si P coincide con C, G coincide también con C y H coincide con A y por tanto

∠(A'G,A'H) = 90°.

P ≡ B

figura 3

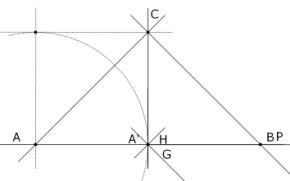
Si P coincide con B; A', G, H coinciden; pero A'G es paralela a AC y A'H es paralela a BC y por tanto

∠(A'G,A'H) = 90°.

P ≡ ∞_CB

figura 4

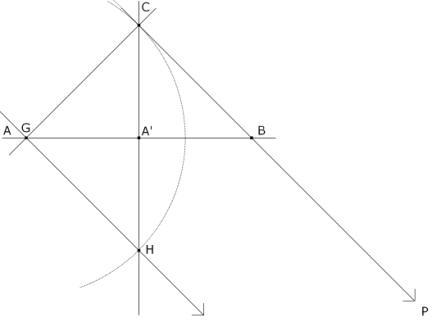
Si P coincide con el punto del infinito de la recta BC; G coincide con A y H coincide con el simétrico de C respecto A' y por tanto

∠(A'G,A'H) = 90°.

Por lo tanto la homografía es la homografía de ángulos rectos con vértice en A' y en consecuencia

∠(A'G,A'H) = 90° ∀ P.