Problema 499
En un triángulo equilátero ABC, Una recta tangente a la circunferencia inscrita corta a AB en P y a AC en Q.
Sea M el punto medio de BC. Demostrar que [ABC]=3( 2[BPM][CQM]/([BPM]+[CQM]) .
Donaire, M.F. (2009): Comunicación personal.
Solución de Martín Acosta Gempeler y el director de la revista
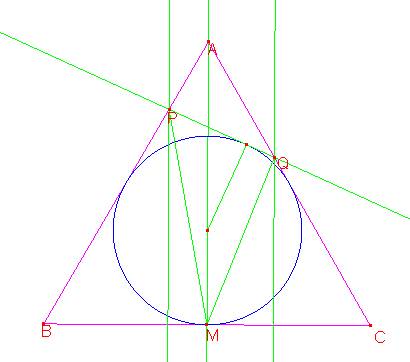
Sean h la altura de ABC, h1 la de BPM y h2 la de MQC:
![]()
Simplificando, es equivalente a:
![]() .
.
Tracemos por el centro del triángulo la perpendicular a la altura AM. Cortará en R a la recta PQ, en S a h1 y en U a h2.
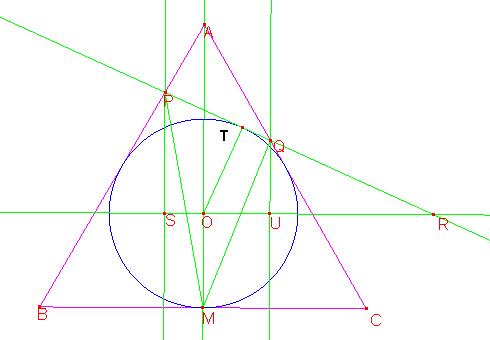
Llamemos D al punto de tangencia con AB y E al punto de tangencia con AC. Vamos a demostrar que la recta TU pasa por el punto E’, simétrico de E con respecto a SU.
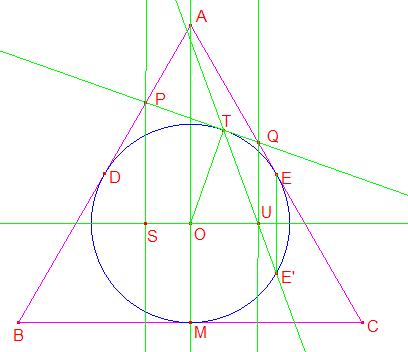
Primero notemos que los triángulos TQO y EQO son congruentes, ya que tienen un lado común OQ, los lados TO y OE son radios del mismo círculo y TQ y QE son tangentes desde el mismo punto.
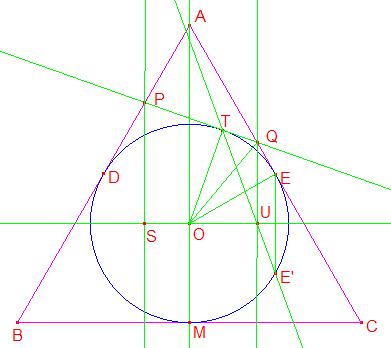
Además, el cuadrilátero TOUQ tiene dos ángulos rectos opuestos (OTQ y OUS), por lo tanto está inscrito en un círculo.
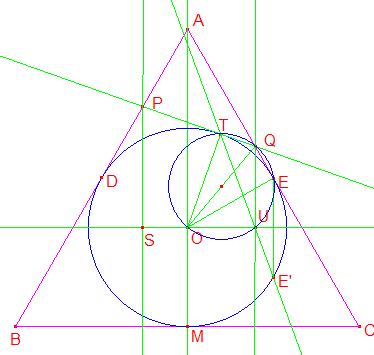
Entonces los ángulos TOQ y TUQ son iguales.
Ahora bien, el ángulo TE’E es la mitad del ángulo TOE, pues este último es ángulo central del mismo arco. Además, el ángulo TOQ es la mitad del ángulo TOE. Por lo tanto, el ángulo TE’E es igual al ángulo TOQ, y al ángulo TUQ. De donde concluimos que la recta TU pasa necesariamente por el punto E’.
Si se analiza la figura con respecto al punto D, se concluye igualmente que la recta TS pasa necesariamente por el punto D’, simétrico de D con respecto a SU.
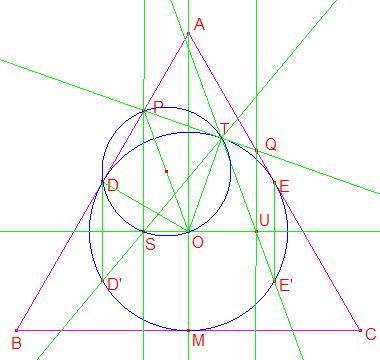
Además, como la altura MO es eje de simetría del triángulo, los puntos D y E están a igual distancia de la recta SU, y por lo tanto los puntos D’ y E’ están sobre una paralela a SU.
En su libro Apollonius Gallus, Vieta
demuestra el siguiente lema: “si
se construye partiendo de los lados de un triángulo una recta paralela a su
base, se obtienen a partir del mismo vértice dos triángulos semejantes. El
círculo circunscrito al primer triángulo será tangente al círculo circunscrito
al segundo triángulo”.
Como hemos demostrado que el triángulo TUS y el triángulo TE’D’ comparten dos lados y el tercero es paralelo, podemos concluir que los círculos TUS y TE’D’ son tangentes.
Sea R el punto de intersección de las rectas QP y US. Los triángulos RUQ, RTO y RSP son rectángulos semejantes.
RT2
=RU RS
QU/OT=OT/RT
PS/RS=OT/RT
De donde:
QU RT = RU OT , es decir: PS QU = OT2
PS RT =RS OT
Por ello:
UQ/TO=
TO/SP.
UQ=h2-h/3,
TO=h/3, SP= h1-h/3.
(h2-h/3)/(h/3)=
(h/3)/(h1-h/3).
Es (h2-h/3)(
h1-h/3) = h2/9.
Es decir, h2h1-h2h/3-hh1/3+h2/9=h2/9.
h2h1=h2h/3+hh1/3
Y por último, es
![]()
Cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.
Martin Eduardo Acosta Gempeler
Doctor en didáctica de las matemáticas
Profesor de