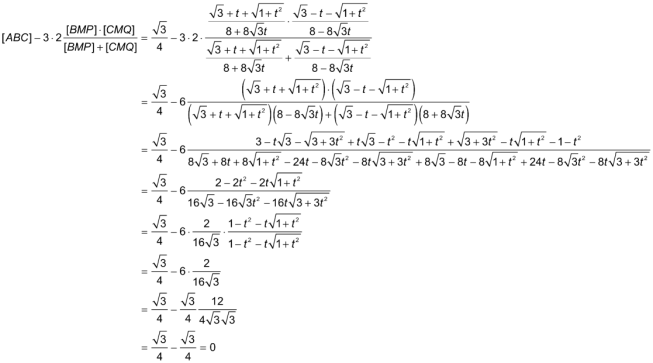Propuesto por Milton Favio Donaire Peña, Estudiante de la Universidad Nacional de Ingenieria Lima - Perú. Facultad de ciencias especialidad Física Pura. Asesor del equipo Olímpico del Perú en el curso de Geometría.

Problema 499. En un triángulo equilátero ABC, Una recta tangente a la circunferencia inscrita corta a AB en P y a AC en Q. Sea M el punto medio de BC. Demostrar que:

[ABC]=3( 2[BPM][CQM]/([BPM]+[CQM]).

Donaire, M.F. (2009): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de marzo de 2009)

Solución

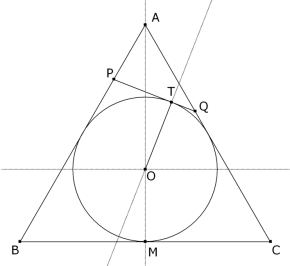
Trazamos la figura de acuerdo con el enunciado.

Si el lado del triángulo equilátero es a, entonces la altura y el radio del círculo inscrito son

.

Si tomamos como sistema de referencia un par de ejes rectangulares con centro en O (centro del círculo inscrito), eje de ordenadas OA y de abscisas la perpendicular por O a OA, podemos escribir:

.

Pero si hacemos, sin pérdida de generalidad, a = 1,

.

Determinamos el punto de tangencia T sobre el círculo inscrito como la intersección de una recta por el origen y el círculo inscrito

.

Determinamos la recta AB

.

Detrminamos la recta AC

.

Como hemos definido la recta OT como una recta cualquiera por el origen, y = t · x, la tangente al círculo circunscrito en el punto T será perpendicular a OT en T y por ello la recta PQ (tangente) será de la forma

;

pero como el punto T también pertenece a la recta, tenemos como recta PQ a:

.

Ahora podemos obtener al punto P como intersección de AB con PQ

y el punto Q como intersección de AC con PQ

.

El área del triángulo BMP es :

.

El área del triángulo CMQ es :

.

Elárea del triángulo ABC es:

.

Para probar el enunciado probaremos que se anula la expresión

.

y sustituyendo valores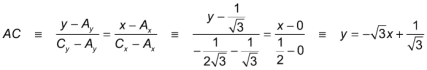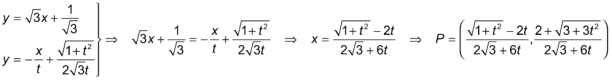
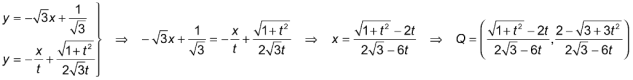