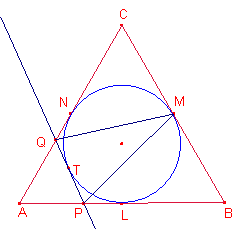
Problema 499

En un triángulo equilátero , una recta tangente a la circunferencia inscrita corta a en el punto P y a en el punto Q.

Sea M el punto medio de . Demostrar que .

Solución de Ricard Peiró:

Supongamos que el lado del triángulo es 1.

.

Sea T el punto de tangencia de la circunferencia inscrita y la recta PQ.

Sea L el punto medio del lado , sea N el punto medio del lado .

Sea, .,

Entonces, ,..

.

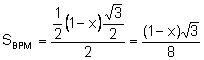Análogamente el área del triángulo es:

.

Aplicando el teorema del coseno al triángulo :

. Simplificando:

(1)

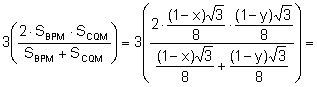
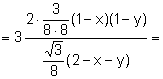
Aplicando (1):

.
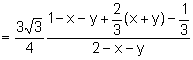
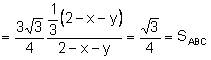