Problema 499.- Propuesto por Milton Fario Peña, estudiante de la Universidad Nacional de Ingeniería Lima-Perú. Facultad de Ciencias, especialidad Física Pura. Asesor del equipo olímpico del Perú, en el curso de geometría.

En un triángulo equilátero ABC, una recta tangente a la circunferencia inscrita corta a AB en P y a AC en Q. Sea M el punto medio de BC. Demostrar que

Resolución: (Vicente Vicario García, I. E. S. El Sur, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo y emplearemos la geometría de coordenadas. Sin pérdida de generalidad, supondremos el lado unidad. A partir de propiedades geométricas elementales, es fácil ver que podemos suponer el triángulo equilátero de coordenadas 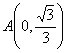,,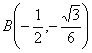, 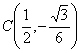y el punto 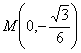. La ecuación de la circunferencia inscrita al triángulo equilátero tendrá entonces por ecuación

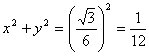
Determinemos inicialmente las coordenadas de los puntos P y Q. Para ello observemos que

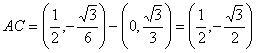
con lo que las ecuaciones de las rectas AB y AC serán entonces las siguientes

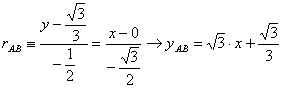
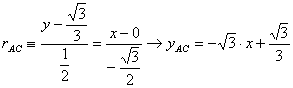
Por otra parte, la ecuación de la recta tangente a la circunferencia inscrita en un punto arbitrario de la misma, se puede determinar fácilmente por derivación implícita, de manera que tenemos

de manera que la ecuación de la recta tangente en T será . Por tanto, teniendo en cuenta que , las coordenadas de los puntos P y Q vendrán dadas por las soluciones de los siguientes sistemas de ecuaciones

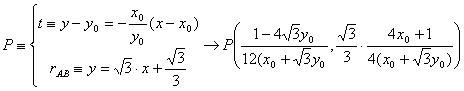
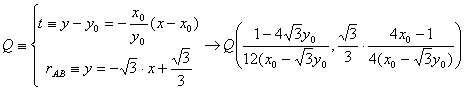
Finalmente evaluemos las áreas de los triángulos BPM y CQM, comprobando la afirmación del enunciado del problema. Es claro que

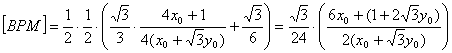
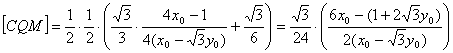
y también tenemos que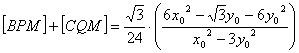

Finalmente, puesto que el área del triángulo equilátero de lado unidad es , y teniendo en cuenta que, tenemos que

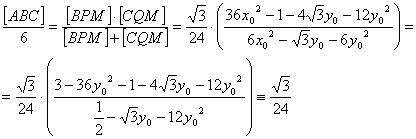
lo que concluye el problema.

---oooOooo---