Problema 1.- (Propuesto por Vicente Vicario García, I.E.S.
El Sur, Huelva).
Probar o refutar las
siguientes proposiciones:
(a) En todo triángulo ABC, al menos uno de los radios de las circunferencias exinscritas 
es mayor o igual que
una de sus alturas 
y recíprocamente.
(b) En todo triángulo ABC se pueden elegir, al menos, dos radios de las circunferencias exinscritas cuyo producto sea
mayor o igual que el producto de dos de sus alturas .
Resolución: (Vicente Vicario García, I.E.S.
El Sur, Huelva)
Utilizaremos
la notación habitual en la geometría del triángulo, siendo 
el área del mismo.
(a) Son bien conocidas las siguientes expresiones clásicas para el área de un triángulo
Se tiene entonces que
Así pues, tenemos que
La
conclusión se sigue razonando por reducción al absurdo, suponiendo que si los tres radios de las circunferencias exinscritas son menores, en
algún orden, que las tres alturas , entonces se tendría, evidentemente que
en contradicción con la igualdad ya demostrada anteriormente. La demostración recíproca es totalmente análoga empleando, de nuevo, la reducción al absurdo.
(b) En realidad probaremos un resultado más fuerte. Demostraremos que se cumple la desigualdad siguiente
Para la
demostración, utilizaremos las expresiones clásicas para el área de un
triángulo del apartado anterior, junto con la fórmula de Herón
y la relación 
Tenemos entonces que
la desigualdad es equivalente a las siguientes:
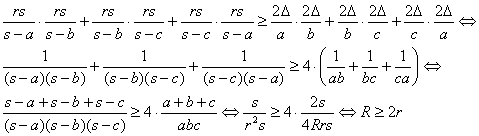
donde la
última desigualdad es la famosa desigualdad de Euler,
que es consecuencia de la desigualdad 
para la distancia
entre el circuncentro y el incentro
de un triángulo.
Finalmente,
sólo resta razonar por reducción al absurdo y suponer que los productos de dos
radios de las circunferencias exinscritas son menores, en
algún orden, a productos correspondientes a dos alturas . En este caso tendremos que se cumpliría
en contradicción con la desigualdad demostrada anteriormente. Esto concluye la demostración.
---oooOooo---
---oooOooo---