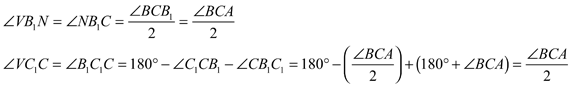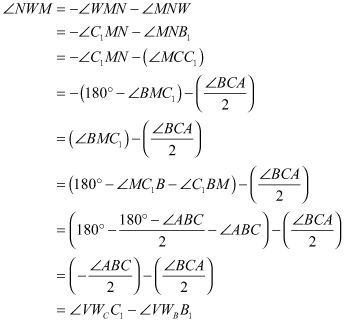Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, 64100 Teramo, Italia.

Problema 502. En un triángulo ABC sean B₁ y C₁ los puntos de intersección de las bisectrices interiores de los ángulos ABC y BCA con AC, AB respectivamente.

Sea V la intersección de B₁. C₁ con BC. Sea W la intersección de las bisectrices de los ángulos VC₁B y VB₁C.

Demostrar que A, V, W están alineados.

Suppa, E. (2009): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). 2 de abril de 2009.

Solución

Sabemos que la alineación de puntos es una propiedad proyectiva; si demostramos el enunciado para el caso en que V es el punto del infinito de BC, el enunciado será cierto para cualquier triángulo.

Para ello, partimos de un triángulo isósceles cualquiera. Al ser ABC isósceles , C₁B₁ es paralela a BC y por lo tanto su punto en común V también será su punto del infinito.

Y trazamos por el vértice A la recta AV paralela a BC que comparte con BC y C₁B₁ el punto del infinito V.

Trazamos la bisectriz del ángulo VC₁B, que encuentra a AV en W_C y a BC en M.

Trazamos la bisectriz del ángulo VB₁C, que encuentra a AV en W_B y a BC en N.

Según el enunciado, las bisectrices C₁W_C y B₁W_C se encuentran en W.

Si demostramos que W_C, W_B y W coinciden, habremos demostrado que W, A, V están alineados.

¡¡¡ Calcularemos los ángulos dirigidos (mód. 180°) tomando como sentido positivo el sentido horario !!!

Veamos ahora que NB₁ es paralela a CC₁

Calculemos el ángulo que forma C₁W_C con AV teniendo en cuenta que C₁W_C es la bisectriz del ángulo VC₁M

Calculemos el ángulo que forma B₁W_B con AV teniendo en cuenta que B₁W_B es la bisectriz del ángulo VB₁N

Calculemos el ángulo NWM que forman las dos bisectrices que se cortan en W

y de aquí

W_C y W_B están sobre la misma recta paralela a BC, luego coinciden; pero si W_C y W_B coinciden , W coincide con ellos, luego W esta en la paralela a BC por A.

W, A y V están alineados en la paralela a BC por A, como la alineación se conserva

proyectivamente, queda probada la alineación de los tres puntos para todo triángulo