Problema 502.- (Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “Albert Einstein”, 64100, Terano, Italia.

En un triángulo ABC sean y los puntos de intersección de las bisectrices interiores de los ángulos ABC y BCA con los lados AC y AB, respectivamente. Sea V la intersección de con BC. Sea W la intersección de las bisectrices y . Demostrar que A, V, W están alineados.

Resolución: (Vicente Vicario García, Huelva)

Representaremos por A, B, C los ángulos del triángulo correspondientes a los vértices del mismo nombre. Resolveremos el problema computando los ángulos necesarios para demostrar la linealidad del segmento requerido por los puntos A, V, W.

Es bien conocido que el ángulo . Denotaremos por y por . Son claros entonces los valores para los siguientes ángulos:

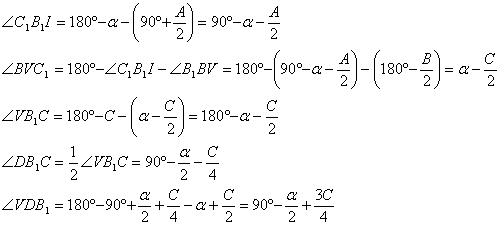
Por otra parte, tenemos que

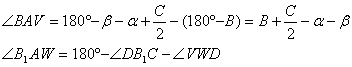
con

Por otra parte, tenemos que

Finalmente, llegamos a

lo que concluye la demostración.

---oooOooo---