Problema 504.- Un triángulo acutángulo ABC está inscrito en una circunferencia de centro O. Las alturas del triángulo son AD, BE y CF. La recta EF corta a la circunferencia en P y Q.

a) Demuestre que OA es perpendicular a PQ.

b) Si M es el punto medio de BC, pruebe que AP ·AP = 2 AD· OM.

Herbert, J. (2000): Revista de Matemática de La Universidad del Zulia Facultad de Ciencias / Departamento de Matemáticas Vol 8, 1

http://www.emis.de/journals/DM/v81/pys.pdf

Solución

a) Por ser AA' un diámetro, < BCA' = 90-<C=<A'AB, y como <AFE=<C necesariamente OA y PQ son perpendiculares.

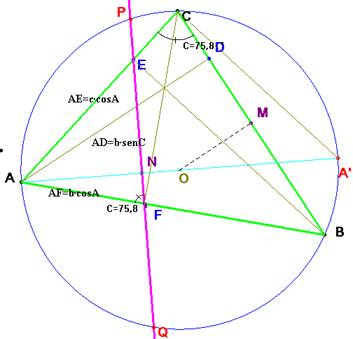
b) Según el teorema del cateto para el triángulo APA' se tiene AP·AP=AN·AA', luego la igualdad a demostrar es equivalente a

AN·AA' = 2AD·OM,

o bien

. (*)

Esto sugiere la posibilidad de que sean semejantes los triángulos ADN y OMA’. En efecto así es: El paralelismo de AD y OM implica que los ángulos en A y en O sean iguales. Completamos la semejanza viendo que los lados correspondientes son proporcionales.

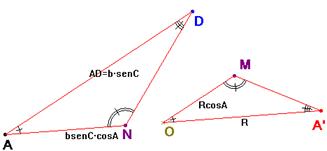De triángulo isósceles OBC resulta que OM=R·cosA, siendo R el radio de la circunferencia circunscrita.

Del triángulo ABC

AF= b·cos A

y del ANF

AN=AF sen C =b·sen C·cos A.

Y con esto queda probado que los lados son proporcionales y que se verifica la igualdad propuesta.