Problema 505.- Dado un triángulo ABC y un punto X sobre la recta BC, se pide:
(a) Inscribir una parábola en los lados del triángulo de manera que X
sea el punto de tangencia con la recta BC.
(b) Demostrar que si Y, Z son los puntos de tangencia con los lados CA,
AB y X', Y', Z' son los simétricos de X, Y, Z respecto de los puntos medios de BC, CA, AB entonces las
rectas AX', BY', CZ' son paralelas al eje de la parábola.
(c) Las rectas isogonales de AX', BY', CZ', es decir las rectas simétricas
de estas rectas respecto de las bisectrices interiores AI, BI y CI, son concurrentes en el foco de
la parábola.
Solución
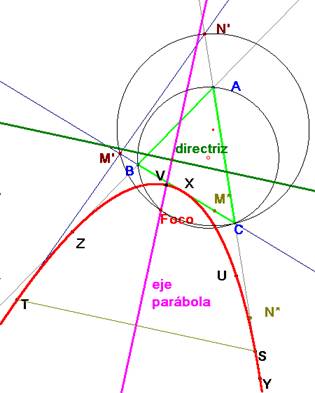
a) Una cónica está determinada por cinco elementos. En este caso tenemos cuatro tangentes (la cuarta es la recta del infinito) y el punto de contacto en una de ellas. La recta del infinito corta a las rectas CB y CA en M y N respectivamente, siendo P el punto de tangencia.
 La
parábola, como cónica formada por sus tangentes, queda definida por la
proyectividad establecida entre las rectas a=CB
y b=CA en la que se corresponden (XMB) y (CNA). El eje de esta proyectividad es la recta XW, obtenida de la unión de los puntos X=XN·MC y W=BN·MA. Con esto podemos hallar todos
los puntos que se deseen. Al punto C,
considerado en la recta a le corresponde
el punto Y de tangencia en b=AC. Y=XW·CA.
La
parábola, como cónica formada por sus tangentes, queda definida por la
proyectividad establecida entre las rectas a=CB
y b=CA en la que se corresponden (XMB) y (CNA). El eje de esta proyectividad es la recta XW, obtenida de la unión de los puntos X=XN·MC y W=BN·MA. Con esto podemos hallar todos
los puntos que se deseen. Al punto C,
considerado en la recta a le corresponde
el punto Y de tangencia en b=AC. Y=XW·CA.
El punto Z se puede obtener aplicando el t. de Brianchon al triángulo circunscrito ABC: las rectas AX, BY y CZ son concurrentes. Otra vez este teorema ahora aplicado al cuadrilátero BMNA nos da P sobre la recta del infinito como proyección desde Z del punto de encuentro de las diagonales AM y BN.
Si queremos otra tangente a la cónica, tomo un punto M' sobre la recta CB, hallamos el homólogo de N' en CA por la proyectividad (XMB) à (CNA) o bien (XBC) à (CAY). Las rectas M'N y MN' se han de cortar sobre el eje XY. Así hallamos N'. El punto común de las diagonales se proyecta por P sobre M'N' en el punto de tangencia T, otra vez por el t. de Brianchon aplicado al cuadrilátero MM'N'N.
Llevamos el problema al plano
afín, donde ya se puede en sentido estricto hablar de parábola. Queremos
calcular el eje de la parábola, el foco y la directriz. Todas las rectas que
pasan por P (punto del infinito) son
diámetros de la parábola.
Partimos de lo conseguido hasta ahora y añadimos a la construcción un quinto punto U a partir de M* sobre CB. Obviamos los detalles de la construcción por no complicar excesivamente la figura.
Para hallar el eje tomo una recta TS, perpendicular a la dirección de los diámetros por T y hallo su corte en la cónica S.
La mediatriz de TS es el eje de la parábola, corta a ésta en el vértice V.
El foco F está sobre el eje y sobre la circunferencia circunscrita a ABC y CM’N’. La directriz es la ortogonal al eje a igual distancia del vértice que el foco.
b) Supongamos que ya tenemos la parábola construida. Podemos
suponer que su ecuación, respecto a ciertos ejes es 2py=x2. El foco de
esta parábola es el punto ![]() , su eje la recta x
= 0 (eje OY )
y su directriz la recta
, su eje la recta x
= 0 (eje OY )
y su directriz la recta ![]() .
.
Si
los puntos de tangencia son 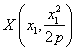 ,
, 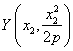 ,
, 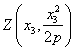 , la ecuación de la tangente en uno de ellos, (es su
polar) es
, la ecuación de la tangente en uno de ellos, (es su
polar) es ![]() . De aquí obtenemos los tres vértices del triángulo tangente:
. De aquí obtenemos los tres vértices del triángulo tangente:
![]() y
y ![]() .
.
A’, el punto medio de BC, tiene coordenadas que son la
semisuma de las de los extremos: ![]() . X’ es
tal que A’ es también el punto medio
del segmento XX’. Con estas premisas
es fácil obtener
. X’ es
tal que A’ es también el punto medio
del segmento XX’. Con estas premisas
es fácil obtener
OX’= 2OA’ – OX = ![]()
que
permite ver fácilmente que la recta AX’
tiene por ecuación ![]() , paralela al eje de la parábola.
, paralela al eje de la parábola.
De igual manera se procede con los otros puntos de tangencia.
c) Sea
A" el pie de la bisectriz del
ángulo CAB. La bisectriz AA" de A sigue siéndolo de AX' y
su simétrica. Es un hecho general que las isogonales de cualesquiera cevianas concurrentes
son otra vez rectas concurrentes. Obviando esta cuestión vamos a centrarnos en
ver que el punto de concurrencia es el foco de la parábola. Sea AF* la
recta isogonal de AX’. Viendo
que F=F*
habremos concluido.
Es un hecho general que las isogonales de cualesquiera cevianas concurrentes
son otra vez rectas concurrentes. Obviando esta cuestión vamos a centrarnos en
ver que el punto de concurrencia es el foco de la parábola. Sea AF* la
recta isogonal de AX’. Viendo
que F=F*
habremos concluido.
Usaremos otra propiedad conocida del foco de una parábola, a saber, que el centro de la circunferencia circunscrita al triángulo formado por tres tangentes también pasa por él. Gracias a esta propiedad, el problema se reduce a demostrar que son semejantes los triángulos AFB y ACX’, pues entonces de la igualdad de los ángulos correspondientes FAB, CAX’ se concluye que AF es la isogonal de AX’. Los referidos triángulos tienen un ángulo igual, el que abarca el arco AB de la circunscrita. Probemos que sus lados son proporcionales:
De los datos obtenidos para los vértices tenemos:
AC = ![]() , CX’=
, CX’= ![]() ,
,
AF = ![]() y BF =
y BF =
![]() .
.
Para evitar raíces cuadradas tomo los cuadrados de las longitudes de estos lados. Después de calcular con paciencia se obtienen:
4p2![]() =
=![]() , 4p2
, 4p2![]() =
=![]() ,
,
4p2![]() =
=![]() , 4p2
, 4p2![]() =
=![]() .
.
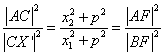
Y con esto se concluye.