Problema 506.- (Propuesto por Vicente Vicario García,
I.E.S. “El Sur”, Huelva).
Sea ABC un triángulo acutángulo. Sea P un punto interior al mismo y 
la suma de las
distancias de P a sus lados. Siendo G el baricentro del triángulo y O su circuncentro, demostrar que:
(a) 
(b) 
Resolución: (Vicente Vicario García, I.E.S. “El Sur”,
Huelva)
Utilizaremos
la notación habitual en la geometría del triángulo. Comenzaremos demostrando un
lema y, a continuación, emplearemos las conocidas desigualdades de Euler 
, y de Gerretsen 
para un triángulo.†
Lema: “En todo triángulo ABC se tiene que 
”.
Demostración: Basta
aplicar la fórmula de Herón y la identidad de Euler 
■
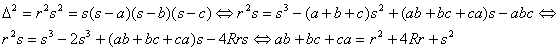
Como
aplicación de la semejanza, y de las propiedades elementales relativas al
baricentro, es claro que la distancia desde el baricentro a un lado del
triángulo, es la tercera parte de la altura correspondiente a ese mismo lado.
Por otra parte, se deduce inmediatamente de la identidad de Euler la conocida relación
que expresa:
“El producto de dos lados de un triángulo es igual al producto de la altura relativa al tercer lado por el diámetro de la circunferencia circunscrita al mismo”.
Así pues, utilizando el lema anterior, tenemos que
; 
Empleando las desigualdades de Gerretsen, entonces
[1]
[2]
y, en consecuencia
Para
demostrar la segunda parte utilizaremos el conocido teorema de Carnot que nos
garantiza que la suma de las distancias del circuncentro O a los lados del triángulo es 
. Existen varias formas de demostrar el teorema, pero una de
ellas es utilizar la conocida identidad
y tener en cuenta que si x, y, z son las distancias del circuncentro a los lados del triángulo, entonces
Finalmente,
demostraremos la desigualdad pedida , a partir de la desigualdad [2], teniendo en cuenta que
y esta última
desigualdad es cierta ya que, por la desigualdad de Euler , tenemos
, y las de Gerretsen de 
, e 
, siendo I, O, G,
H el incentro, circuncentro,
baricentro y ortocentro del triángulo respectivamente.