Problema 507.- Construir un triángulo considerando los segmentos (de las respectivas mediatrices) que unen el circuncentro con los puntos medios de los lados correspondientes.

(Propuesto por Francisco Jara Albarrán, ingeniero agrónomo).

Solución de Francisco Jara Albarrán en el caso del triángulo isósceles

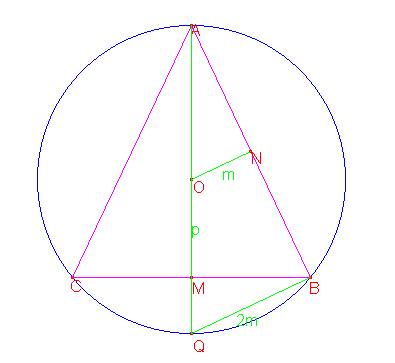
En el caso de triángulo isósceles, llamamos p y m a los segmentos entre el circuncentro y los lados, y R al radio del círculo.

En el triángulo rectángulo ABQ:

AQ * MQ = BQ² es decir 2R * (R – p) = 4 m² , o bien R * (R – p) = 2 m² .

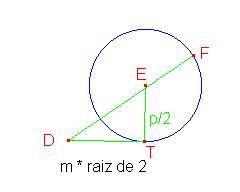
Conocido m es fácil conocer la raíz cuadrada de 2 por m, construyendo un triángulo rectángulo isósceles. Si los catetos miden m la hipotenusa es m por raíz de 2.

Si DT = m * raíz de 2 , trazando una perpendicular en T tomamos un punto E a la distancia p/2, como centro de una circunferencia de radio p/2.

Por potencia desde el punto D se verifica que DF debe ser el valor del radio R ya que R * (R – p) = 2 m²

Una vez conocido R se construye fácilmente el triángulo pedido. Se traza una circunferencia con este radio (ver figura superior del todo). En un diámetro AQ a la distancia OM = p se traza una perpendicular que determina los otros dos vértices B y C