Problema 507.- Construir un triángulo considerando los segmentos (de las respectivas mediatrices) que unen el circuncentro con los puntos medios de los lados correspondientes.

(Propuesto por Francisco Jara Albarrán, ingeniero agrónomo).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema usaremos la notación habitual en la geometría del triángulo. Necesitamos un lema y algunos de sus corolarios, que demostramos a continuación:

Lema: “Sea A un ángulo de un triángulo ABC, entonces es una raíz real de la ecuación algebraica siguiente:

”.

Demostración: Consideremos las relaciones (teorema de los senos generalizado) y (relacionada con el incentro). Utilizando las identidades trigonométricas del ángulo doble, tenemos que

Elevando al cuadrado y operando se tiene

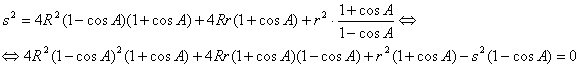
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes en una ecuación algebraica, deducimos a modo de corolario las siguientes relaciones

[1]

que son las relaciones que necesitamos. ■

Centrándonos ya en nuestro problema, es sencillo ver que, utilizando el teorema del ángulo inscrito, los segmentos x, y, z vienen dados por,, . Utilizando estas relaciones y las expresiones [1] deducidas en el lema anterior, llegamos a

[2]

Eliminando entre las dos últimas relaciones en [2], obtenemos fácilmente que

y utilizando la primera de las relaciones [2], la última igualdad se transforma en las siguientes

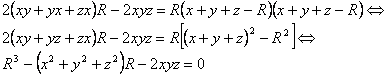
que es una ecuación cúbica en la incógnita R. Es inmediato ver aplicando la regla de los signos de Descartes que la ecuación cúbica anterior admite exactamente una solución real , y además con . Por otra parte (suponiendo a modo de ejemplo valores racionales para x, y, z), de aquí se deduce que, a no ser que esta ecuación cúbica admita una raíz racional, la constructibilidad con regla y compás del triángulo pedido no es posible. Esto no quiere decir que se busquen otros tipos de construcción.

Una forma de construir el triángulo pedido, consiste en estimar el valor de R como raíz real de la ecuación cúbica anterior. Después, consideremos las circunferencias concéntricas centradas en un punto O (circuncentro) y de radios respectivos x, y, z con . Supondremos, sin pérdida de generalidad, que el segmento x es opuesto al vértice A, el y al B, y el z al C. A partir de un punto arbitrario A´ de la circunferencia de radio x, trazamos la tangente a la misma por dicho punto y la prolongamos suficientemente. A continuación, y haciendo centro en O trazamos una circunferencia de radio R que corta a la recta prolongada anterior en dos puntos simétricos que serán los vértices B y C del triángulo buscado. Finalmente, trazando desde C la tangente a la circunferencia de radio y, determinamos el punto de tangencia correspondiente B´ y buscamos el punto simétrico de C respecto de dicho punto B´ obteniéndose el otro vértice A del triángulo pedido. Observemos que al unir A y B por este procedimiento, el segmento ha de ser tangente a la circunferencia de radio z y además en el punto medio C´ de dicho segmento.

---oooOooo---