Problema 508.- Sea ABC
un triángulo, I su incentro y r el radio de su circunferencia
inscrita. Demostrar que se cumplen las siguientes desigualdades:
Resolución: (Vicente Vicario García, I.E.S. “El Sur”,
Huelva)
Utilizaremos
la notación habitual en la geometría del triángulo. Observemos inicialmente que
son todos valores
positivos.
Previamente demostraremos un lema.
Lema: “En todo triángulo ABC se tiene la identidad 
, y análogas expresiones para 
y para 
”.
Demostración: Para demostrar el lema basta emplear el teorema de los senos generalizado, expresiones trigonométricas elementales para los semiángulos del triángulo, y la conocida identidad
[1]
Es
claro que 
, y 
. Por otra parte, tenemos que
y, en consecuencia
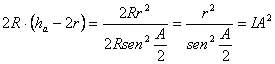
lo que concluye la demostración del lema ■
Para
demostrar la proposición utilizaremos la desigualdad de Erdös-Mordell mejorada,
conocida también como desigualdad de Barrow†.
Además, utilizaremos las expresiones clásicas para la longitud de las
bisectrices interiores de los ángulos de un triángulo. Si denotamos por A´ el punto de corte de la bisectriz
interior del ángulo 
del triángulo BIC
con el lado BC, y tenemos en cuenta
la conocida relación 
, junto con la expresión [1], entonces es claro que
puesto que es claro
que 
, y análogamente para IB´
e IC´.
En consecuencia, aplicando la desigualdad de Barrow (Erdös-Mordell mejorada) y la desigualdad entre las medias aritmética y geométrica, tenemos que
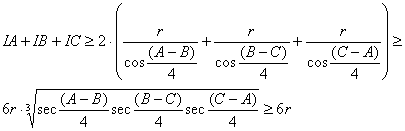
donde la última de las desigualdades es obvia.
---oooOooo---