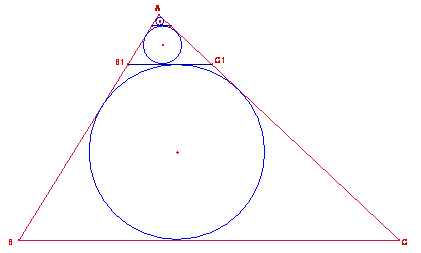
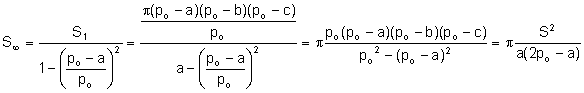Problema 512

Donat el triangle de costats a, b, c es traça el cercle inscrita, i a aquest la recta tangent paral·lela al costat que determina un segon triangle , amb aquest es reitera el traçat anterior, i així successivament. Determineu la suma de les àrees de la successió de cercles inscrits.

Linés, E. y Linés, E. (1949): Ejercicios de Análisis Matemático. Problema 125, pag 175-176.Madrid.

Solució de Ricard Peiró:

Siga S l’àrea del triangle . Siga el radi de la circumferència inscrita al triangle . Siga el semiperímetre del triangle

Siga el radi del triangle . Siga el semiperímetre del triangle .

La circumferència inscrita al triangle és exincrita al triangle .

Aleshores:

.

Vegem que . Ho provarem per inducció:

Per a és certa.

Suposem certa la proposició per a , .

Vegem que pa proposició és certa per a .

La circumferència inscrita del triangle és la exinscrita al triangle .

Els triangles , són semblants. Siga la raó de semblança.

.

Aleshores,

.

Aleshores la successió dels radis és una progressió geomètrica de raó .

Aleshores la successió dels quadrat dels radis és una progressió geomètrica de raó .

La suma de les àrees dels cercles de radis és la suma d’una progressió geomètrica de raó .

Calculem l’àrea del cercle circumscrit al triangle :

Aplicant l’àrea del triangle :

. Aleshores

L’àrea del primer cercle és:

.

La suma infinita de les àrees dels cercles és: