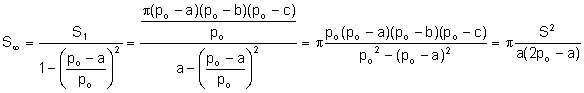Problema 512
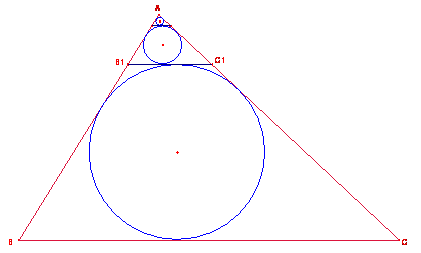
Dado un triángulo ABC de lados a.b.c. se traza el círculo inscrito ; a éste se le tira la tangente paralela al lado a=BC que determina un segundo triángulo AB1C1; con éste se reitera el trazado anterior, y así sucesivamente.Hallar la suma de las áreas de la sucesión infinita de los círculos inscritos.
Linés, E. y Linés, E. (1949): Ejercicios de Análisis Matemático. Problema 125, pag 175-176.Madrid.
Solución de Ricard Peiró:
Sea S el área del triángulo 
. Sea 
el radio de la circunferencia
inscrita al triángulo . Sea 
el semiperímetro
del triángulo
Sea 
el radio del triángulo
. Sea 
el semiperímetro
del triángulo .
La circunferencia inscrita al triángulo es exincrita
al triángulo 
.
Entonces:
.
Veamos que 
. Lo probaremos por inducción:
Para 
es cierta.
Supongamos cierta la proposición para 
, 
.
Veamos que la proposición es cierta para 
.
La circunferencia inscrita del triángulo 
es la exinscrita al triángulo 
.
Los triángulos , son semejantes. Sea 
la razón de semejanza.
.
Entonces,
.
Entonces la sucesión de los radios es una progresión geométrica
de razón 
.
Entonces la sucesión de los cuadrados de los radios es
una progresión geométrica de razón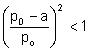 
.
La suma de las áreas de los círculos de radios 
es la suma de una progresión geométrica de razón .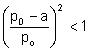
Calculemos el área del círculo circunscrito al triángulo :
Aplicando el área del triángulo :
. Entonces 
El área del primer círculo es:
.
La suma infinita de las áreas de los círculos es:
