Problema 512.- (Propuesto por J. B. Romero Márquez,
profesor colaborador de
Dado un triángulo ABC
de lados a, b, c se traza el círculo
inscrito. A éste se le tira una tangente paralela al lado BC que determina un segundo triángulo 
. Con éste se reitera el trazado anterior y así
sucesivamente. Hallar la suma de las áreas de la sucesión infinita de los
círculos inscritos.
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
A
lo largo de la resolución del problema utilizaremos la notación habitual en la
geometría del triángulo. Es inmediato que los triángulos ABC y son semejantes, ya que
la recta 
es paralela al lado BC. Por otra parte, sean 
, 
, la alturas trazadas desde el vértice A, a los lados BC y , de los triángulos ABC
y , respectivamente. Sean análogamente r, 
los radios de las circunferencias
inscritas a los triángulos anteriores ABC
y , respectivamente y [ABC],
sus áreas. Sea 
la razón de semejanza
para estos triángulos. Es sencillo observar, utilizando las condiciones del
problema y la identidad 
, que tenemos
Es entonces sencillo debido a la semejanza observar que
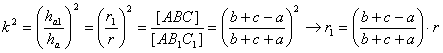
Por otra parte, para la segunda iteración, tenemos que
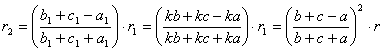, etc.
Por tanto, la suma pedida† es la suma de los infinitos términos de una progresión geométrica infinita de razón menor que la unidad (y por tanto convergente), cuyo valor es bien conocido
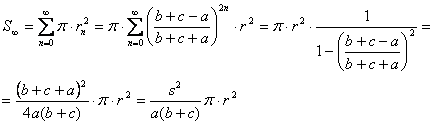
---oooOooo---