Propuesto por Vicente Vicario García, I.E.S. “El Sur”, Huelva.
Problema 513.- Sea ABC un triángulo escaleno y Ng su punto de Nagel. Utilizando la notación habitual en la geometría del triángulo, y suponiendo, (sin pérdida de generalidad) que b > c
1. Demostrar que el triángulo de lados ANg, b-c, 2r, es rectángulo con hipotenusa ANg.
2. Demostrar, como consecuencia del apartado anterior, que un triángulo ABC es isósceles si y sólo si, una al menos, de las distancias entre los vértices del triángulo y su punto de Nagel, es igual al diámetro de la circunferencia inscrita.
Vicario, V. (2009): Comunicación personal.
Solución
1.- El punto de Nagel Ng del triángulo ABC es el incentro del triángulo antimedial A"B"C".
En el problema nº 370 de esta revista está demostrado por el profesor García Capitán cuando dice… ahora podemos considerar I=(a/2:b/2:c/2), N=(s – a: s – b: s – c) y G=(s/3: s/3: s/3), los tres con suma s, y observar que 2I + N = (s: s: s)=3G, para deducir que I, G y N están alineados, cumpliéndose además la relación que IG : IN=1 : 2. (Las coordenadas utilizadas son baricéntricas y s es el semiperímetro del triángulo). Dicho en otros términos: el punto de Nagel es el homólogo del incentro de ABC en una homotecia de centro G (el baricentro) y razón – 2.
Esta propiedad es clave para resolver el problema.
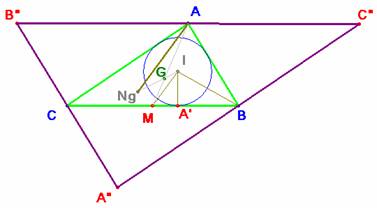
El triángulo rectángulo IA'M, tiene por catetos r=IA' y MA'. CA' = p – c y CM= a/2, luego MA’= (p – c) – a/2 = (b – c)/2. La hipotenusa es la distancia entre el incentro I y el punto medio de BC.
En un triángulo con longitudes el doble de las de éste, la relación se mantiene: los catetos son ahora 2r, b – c y la hipotenusa es la distancia entre su incentro Ng (punto de Nagel de ABC) y el punto medio del lado (punto A), con lo cual queda demostrada esta parte. En general, la hipotenusa es mayor que cualquiera de los catetos, ANg > 2r.
2.- Si el triángulo original es isósceles, el triángulo rectángulo IX’M sobre el lado desigual degenera pues sus vértices están alineados (también con G y con X). Uno de los catetos es cero y la distancia de I a M es el radio r. Al aplicar la homotecia, IM, se transforma en el segmento definido por un vértice y el punto de Nagel. Su longitud es 2r, y se verifica la condición.
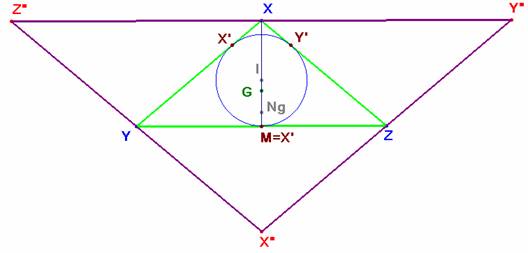
Recíprocamente, si una de las distancias desde un vértice al punto de Nagel es igual al diámetro de la circunferencia inscrita, significa que la hipotenusa del triángulo IA’M o de otro análogo es igual a uno de los catetos. Eso es imposible, salvo si el triángulo degenera: el cateto desigual es nulo, y eso sucede cuando el punto de tangencia coincide con el punto medio, o sea, cuando el triángulo es isósceles.