Problema513 (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva).
Sea ABC un triángulo escaleno y 
su punto de Nagel.
Utilizando la notación habitual en la geometría del triángulo, y suponiendo, (sin
pérdida de generalidad) que 
(a) Demostrar que el triángulo de
lados 
, 
, 
es rectángulo con
hipotenusa .
(b) Demostrar, como consecuencia del apartado anterior, que un triángulo ABC es isósceles si y sólo si, una al menos, de las distancias entre los vértices del triángulo y su punto de Nagel, es igual al diámetro de la circunferencia inscrita.
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva).
(a) Utilizaremos la notación habitual en la
geometría del triángulo. Denotaremos por 
los puntos de corte de
las cevianas Nagel con los lados BC, AC y AB,
respectivamente. Aplicando el conocido teorema de Van Aubel para cevianas
concurrentes y teniendo en cuenta las conocidas posiciones de los puntos de
contacto de las circunferencias exinscritas al triángulo, tenemos que
[1]
Por
otra parte, aplicando el teorema de los cosenos al triángulo 
, tenemos
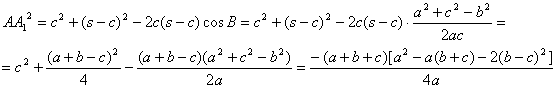
Además, es obvio que 
, y utilizando [1], entonces
y esto implica que tenemos que demostrar la identidad siguiente
[2]
Por otra parte, utilizando
la fórmula de Herón es sencillo determinar 
, que al sustituir en [2], nos da
Finalmente, reduciendo a denominador común, basta demostrar que
que es cierta, como pone de manifiesto un pequeño cómputo algebraico, terminando la demostración.
(b) Este apartado surge como un corolario inmediato de la identidad ya demostrada
ya que si el triángulo
es isósceles (
), es inmediato que 
, y recíprocamente, si , entonces , y el triángulo es isósceles.
---oooOooo---