Problema 514.- Se sabe que la circunferencia circunscrita al triángulo formado por las tres tangentes a la parábola pasa por un punto fijo. ¿Caracteriza esta propiedad a la parábola?.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva).

Inicialmente demostraremos de forma analítica que la circunferencia circunscrita al triángulo formado por tres rectas tangentes a una parábola dada, pasa efectivamente por un mismo punto que es precisamente el foco de la parábola.

Para ello, y sin pérdida de generalidad, podemos suponer el origen de coordenadas como el vértice de la parábola, la recta directriz , y el foco . Es fácil determinar la ecuación de la parábola a partir de su definición como lugar geométrico, siendo P un punto genérico, de modo que

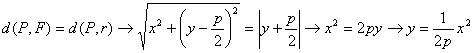
que es la ecuación de nuestra parábola. Sean , ,  tres puntos arbitrarios distintos entre sí de la misma. Determinaremos las ecuaciones de las rectas tangentes a la parábola en estos puntos y las coordenadas del triángulo que forman las mismas. Derivando implícitamente, tenemos la ecuación de la recta tangente a la parábola en el punto de abscisa :

y de forma análoga para las otras dos rectas tangentes. Para determinar las coordenadas de los vértices del triángulo PQR donde se cortan dos a dos estas tangentes basta observar que

                                   

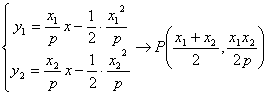
y de forma análoga se obtienen , .

Podemos determinar ahora el circuncentro del triángulo PQR determinando el punto de corte de dos de las mediatrices de sus lados. La expresión de la mediatriz del lado PQ se puede determinar de la forma siguiente

           

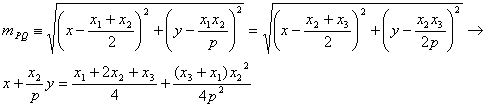
De forma análoga, la ecuación de la mediatriz del lado QR viene dada por

    

Resolviendo el sistema lineal formado por las ecuaciones de estas dos mediatrices, llegamos a obtener las coordenadas del centro O del triángulo PQR

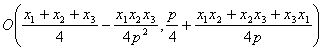
Finalmente, es inemediato llegar a la ecuación de la circunferencia circunscrita al triángulo PQR

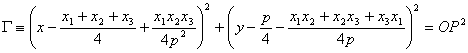
donde es fácil ver que

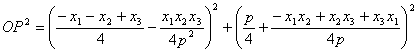
y, por último, es fácil, aunque se requiere un cálculo largo (que se acorta con programas de cálculo simbólico) comprobar que  pertenece a la circunferencia  circunscrita al triángulo PQR. Todo ello se reduce a demostrar la identidad algebraica

            Podemos partir ahora, en lugar de la parábola original, del triángulo formado por tres de las rectas tangentes a esta parábola. De esta forma, podemos caracterizar que el lugar geométrico de los focos de todas las parábolas tangentes a tres rectas no paralelas dadas, corresponde a la circunferencia circunscrita al triángulo formado por las mismas.

            Para la demostración podemos recordar que la tangente en un punto P de una parábola de foco F y recta directriz d es la bisectriz del ángulo formado por la recta FP y la perpendicular a d por el punto P. También utilizaremos el resultado conocido como teorema de Wallace-Simson “Un punto P pertenece a la circunferencia circunscrita a un triángulo ABC si y sólo si las proyecciones ortogonales de F sobre las rectas del triángulo están alineadas”.

            Sea entonces F un punto arbitrario de la circunferencia circunscrita a un triángulo ABC dado y distinto de uno de los vértices. Las proyecciones ortogonales del punto F sobre los tres lados, determinan puntos alineados P´´, Q´´, R´´. Los puntos simétricos del punto F respecto de P´´, Q´´, R´´, serán respectivamente, puntos P´, Q´,R´ que también estarán alineados. La recta d que pasa por estos tres puntos es la directriz de una parábola de foco F que es tangente a los tres lados del triángulo ABC en puntos respectivos P, Q, R. Estos puntos se pueden determinar; por ejemplo P será el punto de corte de la recta correspondiente al lado AB con la perpendicular a la directriz d que pasa por P´, y de forma análoga se encuentran Q y R.

---oooOooo---

Nota 1: Una demostración puramente geométrica de que la circunferencia circunscrita al triángulo formado por tres tangentes a una parábola, pasa por el foco de la misma, se puede ver en la solución al problema 253 sobre ejercicios de cónicas de Ángel Montesdeoca.

Nota 2: La demostración básica de la segunda parte del problema, es decir, el hecho de que el lugar geométrico de los focos de todas las parábolas tangentes a tres rectas no paralelas dadas, corresponde a la circunferencia circunscrita al triángulo formado por las mismas, aparece enunciado como problema 70 en la revista Gaceta Matemática de la RSME (Real Sociedad Matemática Española), con soluciones de Ricardo Barroso Campos (editor de triánguloscabri), F. J. García Capitán, Néstor Aguilera y otros.

Nota 3: Después de la solución que corresponde a la Nota 2 en la revista Gaceta de la RSME se indica que el problema que corresponde a la Nota 1 se atribuye a J. H. Lambert (matemático del siglo XVIII), y que se puede ver una demostración en las páginas 206-208 de la referencia H. Dörrie “100 great problems of elementary Mathematics, their history and solution”, Dover, 1965.