Propuesto por Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

Problema 515.

8.-  Dado un círculo de centro O y un punto A (exterior) hallar el polo, polar o polar recíproco del lugar geométrico de los centros de los círculos circunscritos a los infinitos triángulos autopolares de vértice A, con respecto a la homológica de la circunferencia de centro O, en la homología de vértice A, eje polar de A y recta límite de la primera figura la tangente paralela a la polar de A, no comprendida entre este punto y su polar. Polar del punto A respecto a la homológica de la circunferencia.

Puig Adam, P. (1986): Geometría Métrica, vol. II, pág. 316, nº 8. Propuesto en los exámenes de ingreso a la Escuela de Ingenieros Aeronáuticos, curso 1946-1947.

(.. Me he contentado con sentar las bases indispensables para las más inmediatas aplicaciones y escalar una altura asequible desde la que poder contemplar la Geometría métrica dentro de horizontes más amplios...) Palabras preliminares de la 1ª edición , enero de 1948, Pedro Puig Adam.

Solución

            En primer lugar, por ser la homología  una proyectividad, conserva las relaciones de incidencia, por tanto transformará un haz de rectas en haces de rectas, y por ello, una homología siempre transforma una cónica en otra.

La homológica de la circunferencia es una parábola, pues la recta límite l, la que se transforma en la recta del infinito, es tangente a la circunferencia. Las tangentes desde A a la circunferencia (rectas AK y AI), también serán tangentes a la homológica, y con esto ya conseguiremos dos puntos I y K de la parábola. La unión de los puntos de tangencia nos da la polar de A y por tanto, el eje de la homología. Se pueden hallar las imágenes de otros tres puntos por la homología y completar de este modo la cónica homológica.

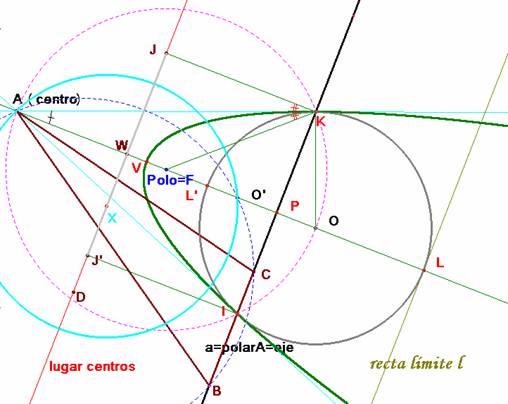
La polar de A es el eje radical de las circunferencias de diámetro AO y la dada.

AO es la mediatriz de KI, se transforma por la homología en el eje de la parábola, según la definición de eje. Los extremos del diámetro LL’ se transforman respectivamente en el vértice V y el punto del infinito A_∞ de la parábola. Tenemos (A P L’ L)=  – 1 (por definición de polar) y  al transformar por la homología (A P V A_∞)=  – 1 que significa que V es el punto medio de AP.

            Sea ABC un triángulo autopolar para la parábola. Los puntos B y C están en el eje de homología, polar de A respecto de la circunferencia y la parábola. Por ello, los triángulos autopolares para la parábola, lo son asimismo para la circunferencia de centro O. Y entonces el ortocentro de esos triángulos es el centro O de ésta (ver problema nº 168 de esta revista). Así pues AP es la altura desde A de TODOS los triángulos autopolares construidos.

La circunferencia circunscrita contiene al simétrico O’ del ortocentro O respecto del lado, por tanto  TODAS las circunferencias circunscritas a los infinitos triángulos autopolares pasan por A y por este otro punto O', simétrico de O respecto a P.  En consecuencia, el lugar geométrico de los centros se encuentra en la mediatriz de AO'. No es toda la mediatriz sino los puntos de ella que están fuera del segmento JJ’, pues para estos puntos la circunferencia centrada en uno de ellos no corta a la polar de A (circunferencia color cyan de centro X), y no se puede encontrar un triángulo autopolar inscrito en ella.

En cualquier otro caso, un punto B de a = polar A junto con A y O’ define una única circunferencia que vuelve a cortar a la polar de A en C, conjugado armónico respecto de I, K pues de lo contrario, si AC* es la polar de B, la c. circunscrita al triángulo autopolar ABC* es la misma que la de ABC y necesariamente C* ha de coincidir con C.

Queremos ver que ese lugar (consideramos toda la recta JJ’) es la directriz de la parábola y su polo el foco F.

            La directriz es una recta perpendicular al eje AO.  K está sobre la circunferencia de diámetro AO. Sea F el centro de la misma. Trazo JK, perpendicular a la directriz. Tenemos los ángulos iguales <JKA = <KAF. Pero también igual a  <AKF por ser F el centro. Como AK es tangente a la parábola, de la igualdad de esos ángulos resulta que F es el foco de la misma, por la propiedad característica de las tangentes a una parábola.  

Si J pertenece a la directriz habremos completado la demostración. Para ello probaremos que JK = WP = radio FK.

WP =AP – AW,   AP = AO – PO,  AW=.

Sustituyendo WP = AP – AW = AO = radio = FK, como queríamos probar.

En una parábola el foco y la directriz son respectivamente polo y polar, y con esto concluimos.