Problema 516

Dato un triangolo rettangolo ABC con l’angolo retto in A. Con P e Q sull’ipotenusa BC tali che BQ = BA e CP = CA, dimostrare che PQ² =2 BP • QC.

Bernd, B.C. (1994): Ramanujan's Noteboooks, Part IV. Springer –Verlag

Solución: Gennaro Rispoli, docente di matematica al Liceo Scientifico 
Sperimentale annesso al Liceo Ginnasio "T.L. Caro", 84087 Sarno 
(Salerno), Italia.

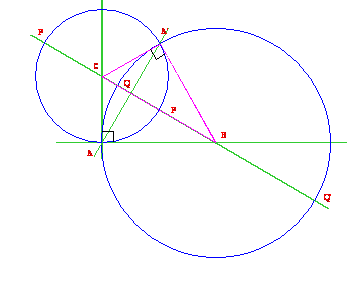
Con riferimento al triangolo ABC mostrato di seguito, abbiamo:

la circonferenza di centro B e raggio BA che interseca BC nel punto Q

la circonferenza di centro C e raggio CA che interseca BC nel punto P

I dimostrazione:

Dal teorema di Pitagora sappiamo che AB²+ AC²= BC²

Essendo AB = BQ = QP + PB, AC= CP = CQ + QP, BC = PB + QP + CQ abbiamo:

 (QP + PB)²+ (CQ + QP)²= (PB + QP + CQ)².

Da tale relazione abbiamo:

QP²+ PB²+2 QP • PB + CQ²+ QP²+2 CQ • QP = PB²+ QP²+CQ²+2 QP • PB +2 PB • CQ+2 CQ • QP

Donde, QP²= 2 PB•CQ.

II dimostrazione:

Dal teorema della secante e della tangente applicato alla circonferenza di centro C, con AB quale tangente in A e BP’ quale secante nei punti P e P’, abbiamo: AB² = BP • BP’.

Essendo AB =BQ, BP’=BP+PP’ abbiamo:

 (BP + PQ)² = BP • BP’= BP • (BP + PP’) = BP • (BP + 2 PQ + 2 QC)

cioè: BP²+ PQ²+2 BP • PQ = BP²+2 BP • PQ +2 BP • QC

Donde, QP²= 2 PB•CQ.