Problema 516

Sea ABC un triángulo rectángulo en A. Tracemos sobre el interior de la hipotenusa BQ=BA, y CP=CA.

Demostrar que PQ²=2BP QC

Bernd, B.C. (1994): Ramanujan's.Noteboooks, Part IV. Springer –Verlag

Solución de Tancredi Nicola ed insegno Matematica e Fisica nel liceo Scientifico "G. Galilei" di Sapri (Sa), Italia. 

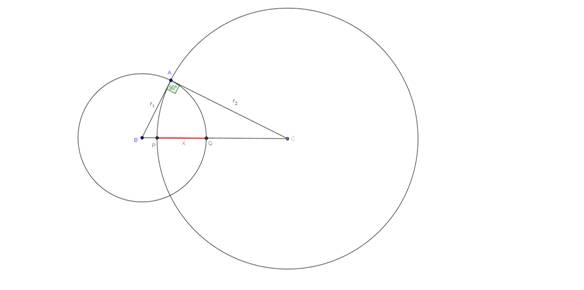
Dato il triangolo rettangolo ABC retto in A. Tracciamo le circonferenze con centri in B e C e raggi di lunghezza pari ai cateti BA e CA rispettivamente. Siano P e Q le intersezioni delle circonferenze con l’ipotenusa BC.

Indichiamo con x il segmento PQ; con r₁ il cateto AB e con r₂ il cateto AC.

Essendo BQ = AB e CP = CA  avremo  e   .

Sviluppando il prodotto      si ottiene

.   (1)

Essendo inoltre l’ipotenusa del triangolo ABC

    (2)

anche la distanza tra i centri delle due circonferenze ortogonali si avrà

  (3)

Uguagliando ed elevando al quadrato la (2) e la (3) si avrà

Semplificando      (4).

Sostituendo la (4) nella (1) si ottiene  da cui

C.V.D.