Problema 517

Eugene Calabi (1923-) encontró en 1997 que además del equilátero, hay otro triángulo  en el que se pueden inscribir tres cuadrados que tienen lados iguales. Uno de los cuadrados se apoya en los tres lados y los otros dos cuadrados tienen cada uno tres vértices sobre los lados del triángulo. En un triángulo fijo dado se pueden inscribir cuadrados... busquemos el mayor posible de lado v... en el triángulo inicial , En el triángulo de Calabi se inscriben  tres con lado v.

Nota del editor 3 de septiembre de 2009

Barthe, D. (2005): Inscrire un carré. Le triangle (Trois points, c'est tout!)

(Bibliothéque tangente, L'aventure mathematique) Éditions Pole. Paris

Solución de Nicola Tancredi ed insegno Matematica e Fisica nel liceo Scientifico "G. Galilei" di Sapri (Sa), Italia. 

Distinguiamo due casi:  triangolo acutangolo o rettangolo e triangolo ottusangolo. Nel primo caso tutti i vertici dei quadrati di area massima inscritti, relativi a ciascun lato, giacciono sui lati del triangolo, nel secondo caso ciò avviene solo per il quadrato che ha il lato sul lato maggiore del triangolo.

A) 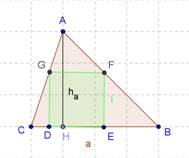   Se il triangolo è acutangolo i tre quadrati inscritti dovranno avere due vertici che cadono internamente ad uno dei lati del triangolo come mostrato nella figura a fianco. Usando la notazione standard e la similitudine dei triangoli ABC e AFG    si ricava

1)     

con   

Dovendo imporre che i tre quadrati inscritti sui tre lati siano uguali si ottengono le seguenti equazioni

Avendo utilizzato le evidenti uguaglianze .  

Il sistema che si ottiene

ha come soluzioni a = b = c (triangolo equilatero).  

Nel caso particolare del triangolo rettangolo isoscele il quadrato di area massima inscritto sull’ipotenusa avrà come lato mentre quello che ha il lato su uno dei cateti avrà lato con   cateto del triangolo.

B) 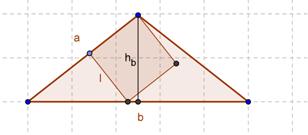    Per simmetria il triangolo ottusangolo dovrà essere isoscele (quadrati di area massima tutti uguali) ed inoltre dovendo essere massima l’area uno dei vertici del quadrato deve coincidere con il vertice del triangolo relativo all’angolo acuto come mostrato in figura. Sfruttando la similitudine dei triangoli rettangoli aventi uno per cateto l’altezza h_b e l’altro il lato l del quadrato si otterrà

     con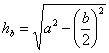        

Inoltre per il quadrato che giace sulla base b deve ancora valere la relazione  1)     . Imponendo che i quadrati siano uguali abbiamo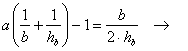     

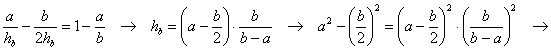
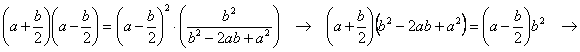
equazione omogenea di terzo grado. Dividendo per a³  e denominando  otteniamo

.

Risolvendo tale equazione graficamente si osserva che esiste una sola soluzione accettabile cioè quella maggiore di uno essendo il triangolo ottusangolo.

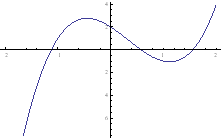
C.V.D.