Problema 517.- Eugene Calabi (1923,-) encontró en 1997 que además del equilátero, hay otro triángulo en el que se pueden inscribir tres cuadrados que tienen lados iguales. Uno de los cuadrados se apoya en los tres lados y los otros dos cuadrados tienen cada uno tres vértices sobre los lados del triángulo.

En un triángulo fijo dado se pueden inscribir cuadrados … busquemos el mayor posible de lado v … en el triángulo inicial. En el triángulo de Calabi se inscriben tres con lado v. (Nota del editor de 3 de septiembre de 2009).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Primero comenzaremos con unos interesantes preliminares y después abordaremos el teorema de Calabi con su demostración.

Preliminares

El problema de inscribir un cuadrado en un triángulo dado tiene una larga historia y debemos remontarnos a los tiempos de Herón de Alejandría, sobre el siglo I de nuestra era. Existen varias formas alternativas (muy conocidas) de inscribir un cuadrado en un triángulo dado. Comentaremos dos de ellas brevemente. Comenzaremos suponiendo que el triángulo dado es acutángulo y más tarde abordaremos los otros dos casos: triángulo rectángulo y triángulo obtusángulo

Forma 1: Sea el triángulo acutángulo ABC. Apoyándonos en el lado BC del triángulo construimos un cuadrado (tendrá un lado sobre este lado del triángulo) que además tendrá un vértice sobre el lado AB (la construcción es extremadamente sencilla pues basta con trazar una perpendicular al lado BC y prolongar hasta construir el cuadrado) aunque su cuarto vértice sea interior al triángulo de partida. Posteriormente, construimos otro cuadrado distinto al anterior con la misma filosofía. Finalmente, basta trazar la línea que une los dos vértices libres de los dos cuadrados así construidos, hasta cortar al lado AC del triángulo original. Este último punto de corte será uno de los vértices del cuadrado inscrito buscado que se apoya sobre un lado del triángulo original.

Observemos que esta configuración la podemos efectuar tres veces, una para cada lado. Por otra parte, los tres cuadrados que se pueden inscribir en el triángulo acutángulo, apoyándose cada uno de ellos sobre cada uno de los lados del triángulo original, en general, son de distinta dimensión. En realidad, como demostraremos a continuación, el mayor cuadrado inscrito lo será sobre el lado menor del triángulo de partida.

Forma 2: Otra construcción extremadamente sencilla se puede ver en los trabajos de Floor van Lamoen en la revista digital Forum Geometricorum (2004-24). Para construir un cuadrado inscrito en un triángulo acutángulo sobre un determinado lado del mismo, digamos BC, se construye exteriormente sobre este lado un cuadrado. Basta entonces con unir los dos vértices exteriores del mismo con el vértice opuesto A del triángulo para obtener dos puntos de corte sobre el lado BC. Trazando perpendiculares sobre estos dos puntos se tiene la construcción buscada.

A continuación veremos dos lemas importantes que arrojan algo de luz sobre las dimensiones de estos cuadrados inscriptibles.

Lema 1: “Sea un triángulo ABC con  y  las alturas respectivas sobre cada uno de estos lados. Entonces se tiene la cadena de desigualdades siguiente: ”.

Demostración: Basta observar que si , tenemos claramente que

    ■

Lema 2: “Sea un triángulo acutángulo ABC. Entonces el lado del cuadrado inscrito en este triángulo con uno de sus lados apoyándose sobre el lado BC tiene como valor  ”.

Demostración: Sea x la longitud del lado del cuadrado inscrito. Este cuadrado divide el triángulo original en cuatro regiones. (tres triángulos y el propio cuadrado) Por consideraciones de áreas de figuras elementales tenemos claramente que

                            ■

Ahora es claro, según los lemas anteriores, que si , entonces tenemos que

           

con lo que el cuadrado inscrito mayor lo es sobre el lado menor de triángulo de partida.

Por otra parte, en un triángulo rectángulo sólo es posible inscribir dos cuadrados diferentes: uno el que se apoya sobre la hipotenusa, y el otro que tiene un vértice que corresponde al vértice del ángulo recto del triángulo de partida y se apoya en cada uno de sus catetos.

En un triángulo obtusángulo, podemos inscribir el cuadrado que se apoya en el lado mayor (opuesto al ángulo obtuso) e inscribir otros dos cuadrados que se apoyan en los otros lados y que tienen un vértice colgando no inscrito.

El triángulo de Calabi

Sabemos, por lo comentado anteriormente, que hay exactamente tres modos en los que un cuadrado se puede inscribir en un triangulo dado. El caso excepcional ocurre cuando tenemos un triángulo rectángulo. En este caso la comparación de los lados de los dos posibles cuadrados es sencilla. El cuadrado que se apoya en cada uno de los dos catetos es siempre mayor que el que se apoya sobre la hipotenusa. Por tanto, el cuadrado inscrito mayor en este caso, es único.

Si el triángulo es acutángulo, ya hemos comentado que tenemos tres cuadrados inscritos posibles y el mayor se apoya sobre el lado menor del triángulo original. Por tanto, si el triángulo no es isósceles, el cuadrado inscrito mayor es también único.

La situación es diferente si el triángulo es obtusángulo. Sea A el vértice que corresponde al ángulo obtuso. Si suponemos que el triángulo no es isósceles, entonces tendremos, sin pérdida de generalidad, que si , es fácil ver que el cuadrado inscrito que se apoya sobre el lado AC es mayor que el que se apoya sobre el lado AB. De este modo, de nuevo tenemos la imposibilidad de tres cuadrados inscritos de la misma área. Por otra parte, y de manera intuitiva, vemos que si el ángulo recto es sólo ligeramente mayor que un recto entonces el cuadrado inscrito que se apoya sobre el lado BC será menor que el mayor de los otros dos cuadrados inscritos que se apoyaban en cada uno de los lados que formaban el ángulo obtuso. Además si el ángulo obtuso es de gran amplitud, se observa fácilmente que ahora el cuadrado inscrito de mayor área será el que se apoya sobre el lado BC. También entonces deben existir estados intermedios en los que es posible la igualdad de las áreas de los dos cuadrados considerados anteriormente.

Caractericemos ahora el triángulo de Calabi. Sea y la longitud del lado de cada uno de los cuadrados inscritos en el mismo. Sea x la longitud de cada uno de los lados iguales del triángulo isósceles que configuran el triángulo. Sean a y  el lado desigual y la altura relativa al mismo. Entonces es fácil verificar que se tiene

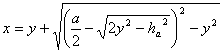                                                     [1]

Además sabemos, por lo comentado en los lemas anteriores que    

Por otra parte, aplicando el teorema de Pitágoras tenemos que. Entonces, sustituyendo esta última expresión en [1], tenemos que

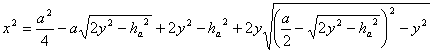
y sustituyendo el valor de y, llegamos a

Finalmente, multiplicando ambos miembros por  y denotando , y dividiendo posteriormente por , llegamos, después de simplificar, a la ecuación siguiente

Recurriendo al archiconocido y (muy sencillo de manejar) programa de cálculo simbólico DERIVE, llegamos a la solución aproximada siguiente

que define y caracteriza al triángulo de Calabi.

Nota: Por supuesto existen multitud de formas de caracterizar el triángulo de Calabi distintas de la anterior y, evidentemente, equivalentes a ella.

---oooOooo---