Problema 518

Propuesto por Juan Bosci Romero Márquez, profesor colaborador de la Universidad de Valladolid

Sea  ABC un triángulo con ángulo mayor en A, y lados a ³ b ³ c . Tracemos sobre el interior del lado mayor BC opuesto al ángulo A, los puntos P y Q tales que BP=a-b y QC=a-c.

Sean las alturas trazadas desde los vértices P y Q de los triángulos ABP y ACQ y sus pies P´y Q´sobre sus lados opuestos AB y AC respectivamente.

Probar que :

a)   

b)      

c) Son a) y b) dos caracterizaciones equivalentes de la clase de triángulos según los ángulos?

Romero, J.B. (2009): Comunicación personal

Solución de Gennaro Rispoli, docente di matematica al Liceo Scientifico 
Sperimentale annesso al Liceo Ginnasio "T.L. Caro", 84087 Sarno 
(Salerno), Italia.

Considerazioni preliminari

Con BC = a, CA = b, AB = c, costruiamo la circonferenza di centro B e raggio c e quella di centro C e raggio b ottenendo i punti P e Q su BC. Così abbiamo BP = a-b e QC =a-c.

Abbiamo inoltre PQ =a-BP-QC=a-(a-b)-(a-c)=b-a+c.

Fig.518/1

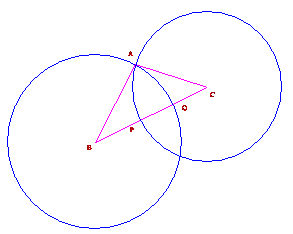
Situazione problematica posta al punto a)

Con PQ = b-a+c,  BP = a-b e QC =a-c abbiamo intanto:

 PQ²=b²+ a²+ c²-2ba+2bc-2ac e 2 BP QC= 2(a-b)( a-c)= 2( a²-ac-ba+bc)

Caso del triangolo rettangolo. ÐA= 90°.

Se ÐA= 90° abbiamo a²=b²+ c² per mezzo del teorema di Pitagora.

 Così abbiamo:

PQ²= b²+ a²+ c²- 2ba + 2bc -2ac = b²+ b²+ c²+ c²-2ba+2bc-2ac =2( b²+ c²-ba+bc-ac) e

2 BP QC= 2( a²-ac-ba+bc)=2(b²+ c²-ac-ba+bc).

 Pertanto la differenza di tali espressioni è uguale a 0. PQ²-2 BP QC =0.

Se invece PQ²-2 BP QC =0,  cioè b²+ a²+ c²- 2ba + 2bc -2ac -2( a²-ac-ba+bc) =0 abbiamo b²+ a²+ c²= 2 a²  cioè b²+ c² = a². Pertanto il triangolo è rettangolo. ÐA= 90°.

La situazione con Cabri è quella mostrata di seguito. Fig. 518/2.

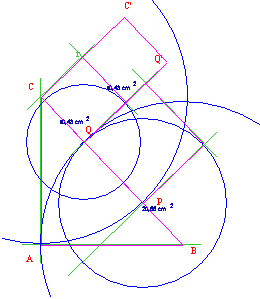
Caso del triangolo ottusangolo. ÐA > 90°.

Con le dovute semplificazioni l’espressione PQ²-2 BP QC diviene b² + c²- a². Dal teorema del coseno o teorema di Carnot (Lazare- Nicolas, 1753-1823) abbiamo a²= b²+ c²- 2bc cos( ÐA). Pertanto l’espressione b² + c²- a² diviene 2bc cos( ÐA).

Se ÐA >90° abbiamo cos( ÐA) <0 allora 2bc cos( ÐA)< 0. Se invece 2bc cos( ÐA) <0 abbiamo  cos( ÐA) <0 ovvero ÐA >90°.

La situazione con Cabri è quella mostrata di seguito. Fig. 518/3.

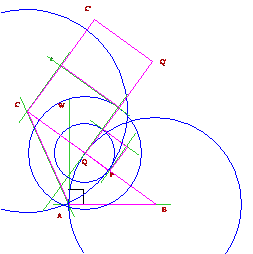
Caso del triangolo acutangolo. ÐA < 90°.

Valgono considerazioni analoghe a quelle appena trattate.

Situazioni problematiche poste ai punti b) e c)

Costruiamo in primis  le altezze h_P =PP’e h_Q =QQ’dei triangoli indicati APB e ACQ, poi due circonferenze, una di centro P e raggio PP’ e l’altra di centro Q e raggio QQ’. Vediamo che la situazione proposta diviene un problema di posizioni reciproche di due circonferenze, che possono essere tangenti esternamente o secanti o esterne. La retta PQ diviene la retta dei centri di tali circonferenze, la retta tracciata per gli eventuali punti comuni è invece l’asse radicale delle stesse circonferenze.

Caso del triangolo rettangolo. ÐA= 90°.

Consideriamo la retta AA’ asse radicale delle circonferenze originarie che individuano i punti P e Q situati sul lato BC. Così AA’C e ABA’sono triangoli isosceli che condividono il lato AA’.

Sia H inoltre il punto di intersezione di AA’ con BC. Vediamo che le circonferenze aventi rispettivamente come centri P e Q e raggi h_P =PP’e h_Q =QQ’ sono tangenti esternamente. Pertanto la distanza tra i centri P e Q è uguale alla somma dei raggi h_P =PP’e h_Q =QQ’. Donde la tesi.

Fig.518/4

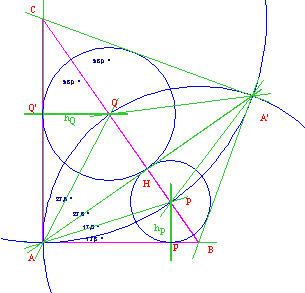
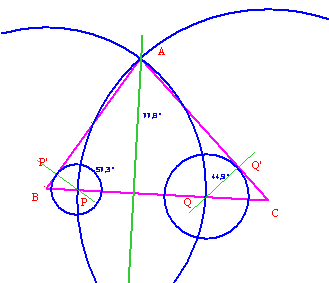
Caso del triangolo ottusangolo. ÐA > 90°.

Vediamo che le circonferenze aventi rispettivamente come centri P e Q e raggi h_P =PP’e h_Q =QQ’ sono secanti. Pertanto la distanza tra i centri P e Q è minore della somma dei raggi h_P =PP’e h_Q =QQ’. Donde la tesi.

Fig.518/5

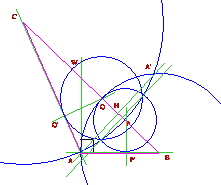
Caso del triangolo acutangolo. ÐA < 90°.

Vediamo che le circonferenze aventi rispettivamente come centri P e Q e raggi h_P =PP’e h_Q =QQ’ sono esterne. Pertanto la distanza tra i centri P e Q è maggiore della somma dei raggi h_P =PP’e h_Q =QQ’. Donde la tesi.

Fig. 518/6

Le riflessioni esposte sopra risolvono anche la questione posta al punto c).