Problema 519.

Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, 64100 Teramo, Italia

Una circunferencia que pasa por el vértice A de un triángulo ABC, interseca el lado AB en P, y el  lado AC en Q .

Tomamos dos puntos, M sobre PB y N sobre QC tales  que PM:MB = QN:NC.

Demostrar que las circunferencias circunscritas a los triángulos APQ, AMN, ABC concurren en un punto X (con X distinto de A).

(Nota del proponente: La recta PQ no debe ser paralela a BC. 17 de Septiembre de 2009)

Suppa, E. (2009) Comunicación personal.

Solución del director de la revista.

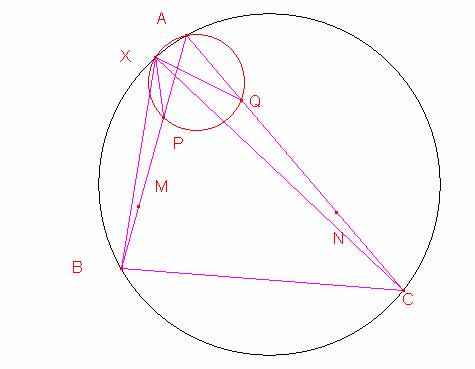
Tenemos en los triángulos XQC y XPB:

<QXP=<QAP (por subtender el mismo arco en la circunferencia circunscrita a APC )→ <QXP=<CAB=<CXB.   

<QXC=<QXP-<CXP=<CXB-<CXP=<PXB.

<ACX=<ABX (por subtender el mismo arco XA en la circunferencia circunscrita a ABC)→<QCX=<PBX.

Así los triángulos XQC y XPB son semejantes siendo X el centro de semejanza que es composición de un giro de ángulo <BAC y una homotecia de centro X y razón y por tanto son QC/PB.

Si se traza el triánguloXC*Q* girado del XCQ un ángulo <BAC, se tiene que el punto N se transforma en N*por ser PM:MB = QN:NC, es

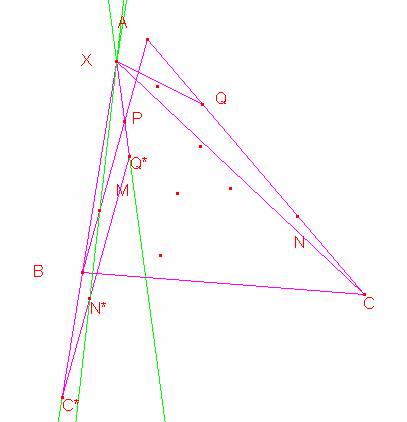
Los puntos X, M, y N* están alineados, y tenemos <MXP=<N*XQ*,  <MXB=N*XC*, y <XMP=<XN*Q*.

Por tanto  <XMP=<XNQ→<XMA=<XNA, así MNAX son concíclicos cqd.

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla.