Problema 519.
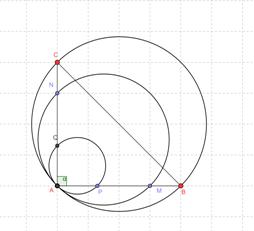
Una circunferencia que pasa por el vértice A de un triángulo ABC, interseca el lado AB en P, y el lado AC en Q . Tomamos dos puntos, M sobre PB y N sobre QC tales que PM:MB = QN:NC. Demostrar que las circunferencias circunscritas a los triángulos APQ, AMN, ABC concurren en un punto X (con X distinto de A).
(Nota del proponente: La recta PQ no debe ser paralela a BC.)
Solución de Nicola Tancredi ed insegno Matematica e Fisica nel liceo Scientifico "G. Galilei" di Sapri (Sa), Italia.
LEMMA 1
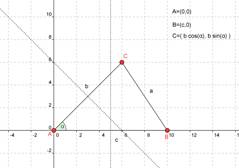 Dato un triangolo ABC posto in piano cartesiano con il vertice A
nell’origine degli assi il vertice B sull’asse x ed il vertice C in un generico
punto del piano cartesiano. L’equazione della circonferenza circoscritta al
triangolo avrà equazione
Dato un triangolo ABC posto in piano cartesiano con il vertice A
nell’origine degli assi il vertice B sull’asse x ed il vertice C in un generico
punto del piano cartesiano. L’equazione della circonferenza circoscritta al
triangolo avrà equazione
![]()
Dove b e c sono le lunghezze dei due lati del triangolo con vertice in
A ed a è
l’angolo compreso tra i due lati (![]() ). Se
). Se ![]()
si avrà semplicemente ![]()
DIMOSTRAZIONE
Passando per l’origine degli assi il termine noto è nullo.
Le coordinate del centro si ottengono mettendo per esempio a sistema gli assi relativi ai lati AB e AC.
![]()
Ne segue che l’ascissa del centro è ovviamente c/2 essendo AB sull’asse delle ascisse mentre l’ordinata sarà
![]() dopo semplici calcoli.
Il caso
dopo semplici calcoli.
Il caso ![]() è facilmente
verificabile.
è facilmente
verificabile.
LEMMA 2
Dato un segmento AB di lunghezza c . Sia P un punto di AB tale che AP = r e sia M un punto che divide PB in
modo tale ![]() . Allora il segmento
. Allora il segmento ![]()
DIMOSTRAZIONE
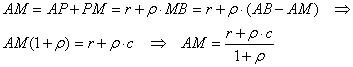
 DIMOSTRAZIONE
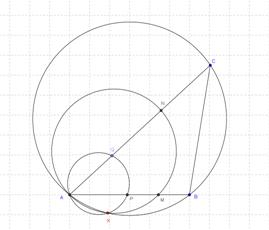
DEL PROBLEMA
DIMOSTRAZIONE
DEL PROBLEMA
Dal LEMMA 2 definito ![]() si avrà
si avrà
![]() e
e ![]()
dove ![]() e
e ![]()
Dal LEMMA 1 l’equazione della circonferenza passante per A, M ed N sarà
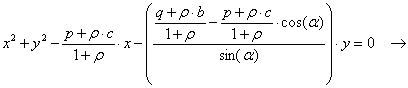
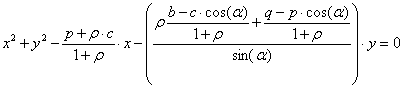 (1)
(1)
Tale equazione è proprio il fascio delle circonferenze generate dalle circonferenze passanti per ABC e per APQ di parametro r perciò passerà per i punti comuni alle circonferenze generatrici.
Infatti sempre dal LEMMA 1 l’equazione della circonferenza per ABC sarà
![]() (2)
(2)
Mentre quella passante per APQ sarà
![]() (3)
(3)
Moltiplicando per r la (2) , sommando l’ equazioni così ottenuta con la (3) e dividendo per (1+r) si ottiene l’equazione (1) , che perciò rappresenta il fascio di circonferenze generato dalla (2) e dalla (3).
C.V.D.
OSSERVAZIONE
Se il triangolo è rettangolo isoscele cioè a = 90° e b = c = l le equazione
delle circonferenze (1) e (2) e (3)
saranno del tipo ![]() . Le circonferenze passanti per APQ e per AMN sono tangenti
internamente alla circonferenza passante per ABC nel punto A che sarà l’unico in comune delle tre circonferenze.
La retta tangente ha equazione y = -x .
. Le circonferenze passanti per APQ e per AMN sono tangenti
internamente alla circonferenza passante per ABC nel punto A che sarà l’unico in comune delle tre circonferenze.
La retta tangente ha equazione y = -x .