Problema 520
Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva
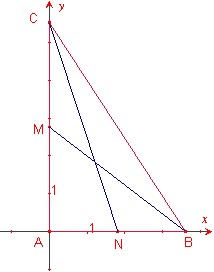 De entre todos los triángulos rectángulos con hipotenusa fija a,
determinar aquel tal que el ángulo agudo formado por las medianas que parten de
los vértices correspondientes a los ángulos agudos del mismo, sea máximo.
De entre todos los triángulos rectángulos con hipotenusa fija a,
determinar aquel tal que el ángulo agudo formado por las medianas que parten de
los vértices correspondientes a los ángulos agudos del mismo, sea máximo.
Vicario, C. (2009) Comunicación personal.
.
Solución de Ricard Peiró i Estruch.
Siga el triángulo rectángulo ![]() ,
, ![]() , tal que
, tal que ![]() fijo con las siguientes
coordenadas cartesianas:
fijo con las siguientes
coordenadas cartesianas:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Las coordenadas de los puntos medios de los catetos son:
![]() ,
, 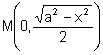 .
.
El ángulo agudo que formen les medianas ![]() es igual al ángulo que
forman los vectores
es igual al ángulo que
forman los vectores ![]() .
.
Determinemos las componentes de los vectores:
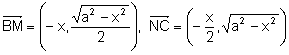 .
.
Utilicemos el producto escalar de los vectores para calcular el coseno del ángulo que forman:
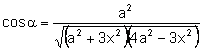 .
.
El valor máximo del ángulo ![]() se alcanza para al
valor máximo de la función
se alcanza para al
valor máximo de la función ![]() ,
, ![]() .
.
![]()
![]() si
si ![]() ,
, ![]() .
.
![]()
![]() , entonces,
, entonces, ![]() es un mínimo. En este
caso no existiría el triángulo.
es un mínimo. En este
caso no existiría el triángulo.
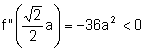 , entonces,
, entonces, ![]() es un máximo. En este
caso el triángulo es rectángulo y isósceles.
es un máximo. En este
caso el triángulo es rectángulo y isósceles.