Problema 520

Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva

De entre todos los triángulos rectángulos con hipotenusa fija a, determinar aquel tal que el ángulo agudo formado por las medianas que parten de los vértices  correspondientes a los ángulos agudos del mismo, sea máximo.

Vicario, C. (2009) Comunicación personal.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo, de modo que A sea el ángulo recto. A partir del teorema de Pitágoras, bastará considerar uno de los dos catetos como variable (nosotros consideraremos, sin pérdida de generalidad, el cateto b). Obviamente, el problema es de máximo, porque basta considerar un triángulo con uno de los catetos de longitud muy próxima a la hipotenusa para comprender que el ángulo que forman las medianas  que parten de sus ángulos agudos va decreciendo paulatinamente.

A partir de la fórmulas clásicas para las medianas de un triángulo a partir de sus lados, (o a partir del teorema de Pitágoras) es inmediato llegar a las expresiones

Sea G el baricentro del triángulo rectángulo ABC de partida. Sean B´ y C´ los puntos medios de los lados AC y AB, respectivamente y  el ángulo agudo formado por las medianas que parten de B y C. Consideremos el triángulo BGC´ y apliquemos el teorema de los cosenos al mismo. Entonces, tenemos que

Entonces, después de sustituir y simplificar, llegamos a

Podemos observar que el numerador de la última expresión es constante, ya que la longitud de la hipotenusa a lo es. Entonces, para que el ángulo sea máximo, debemos buscar cuándo  es mínimo. En consecuencia, bastará maximizar la función subradical del denominador haciendo  con .

Claramente la función  es una función continua y derivable en el dominio . Determinando su primera y segunda derivadas tenemos que

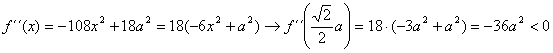
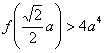Finalmente, comparando con los valores en los extremos y  y teniendo en cuenta que , llegamos a la conclusión de que entre todos los triángulos rectángulos con hipotenusa de longitud fija, aquel que tiene medianas que parten de los ángulos agudos y forman ángulo máximo es el triángulo rectángulo isósceles. Así pues, en esta situación .

Por otra parte, podemos ahora determinar fácilmente el valor del ángulo máximo buscado, que será

                         

---oooOooo---