Problema 521.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva).

Sea ABC un triángulo. Sea K el simediano (o punto de Lemoine-Grebe) del mismo. Consideremos las simedianas BK y CK que parten de sus vértices B y C, respectivamente. Demostrar que si estas simedianas son perpendiculares entonces tenemos que

(a)           

(b) Uno de los ángulos B ó C es obtuso

(c) Siendo G el baricentro del triángulo se cumple que

Nota: El propósito de este problema surge de la búsqueda de demostraciones de algunos apartados sobre triángulos especiales de los artículos (Triángulos especiales I, II y III de D. Francisco Bellot en la revista digital OIM). En particular, estas propiedades son enunciadas, pero no demostradas, en este bello y erudito trabajo. Triángulos especiales III. Apartado III. 19. El triángulo con dos simedianas perpendiculares.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Sean A´, B´ y C´ los pies de las simedianas que parten de los vértices A, B y C del triángulo, respectivamente. Emplearemos también las expresiones clásicas para las longitudes de las medianas  y   y las simedianas  y de un triángulo cualquiera, en función de los lados del mismo

(a)

Necesitaremos aplicar ahora el teorema de Von Aubel para cevianas concurrentes en un triángulo, particularizado para el punto simediano del mismo. Con la notación introducida, este teorema afirma que

Por otra parte, es bien conocida la relación (teorema de Steiner) entre las simedianas en un triángulo (que se cumple realmente en toda su generalidad para cevianas isogonales)

                                                   [1]

Así pues, efectuando los cálculos oportunos podemos llegar fácilmente a las relaciones clásicas siguientes

                                                        [2]

Imponiendo ahora la condición de perpendicularidad de las simedianas BK y CK, es decir, que el triángulo KCB´ sea rectángulo en K, tenemos por el teorema de Pitágoras que . Podemos utilizar las relaciones [2] y las expresiones obvias , y . Además, podemos calcular B´C en función de los lados del triángulo original a partir del mencionado teorema de Steiner [1], obteniendo fácilmente que

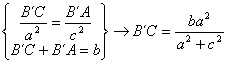
y, en consecuencia

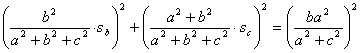
            Introduciendo los valores de las simedianas, en función de los lados queda

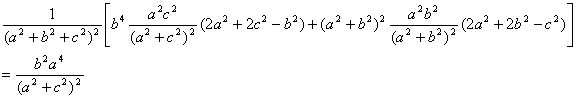
            Multiplicando por , tenemos que

que se puede factorizar en la forma

y de donde se deduce el resultado buscado.

(b)

Para demostrar que uno de los ángulos B o C es obtuso procederemos a razonar por reducción al absurdo, suponiendo que ninguno de ellos lo es y llegando a una contradicción. Supondremos, sin pérdida de generalidad, que  Es claro que si B no es obtuso, se tiene que . Aplicando ahora la relación , tenemos que , lo que es absurdo.

(c)

Para demostrar que , utilizaremos la fórmula de Herón para el área de un triángulo y el hecho bien conocido de que el área del triángulo BGC es la tercera parte del área del triángulo original ABC. Entonces, utilizando propiedades elementales de las medianas, es claro que

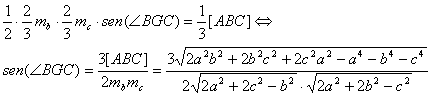
Teniendo en cuenta que , bastará con demostrar que

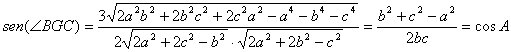
y, elevando al cuadrado y simplificando llegamos a

Sustituyendo  y simplificando, todo se reduce a demostrar la identidad algebraica

que tras un poco de cálculo se demuestra fácilmente que es cierta.

---oooOooo---