Problema 522- Sea ABC un triángulo acutángulo. Una circunferencia w es tangente a AB y a AC en P y Q respectivamente, y también es tangente a la circunferencia circunscrita a ABC en un punto S. Demostrar que el punto medio de PQ es el incentro de ABC.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Denominaremos O al centro de la circunferencia circunscrita al triángulo ABC, O´ al centro de la circunferencia w del enunciado del problema y D será el punto de corte de la bisectriz interior del ángulo A (distinto del propio A) con la circunferencia circunscrita al triángulo ABC (que es bien conocido que cae sobre el punto medio del arco BC). Necesitamos previamente tres lemas, que demostramos a continuación:

Lema 1: “En todo triángulo ABC se cumple la identidad ”.

Demostración: Por consideraciones y recursos trigonométricos elementales, y empleando el teorema de los senos generalizado, es claro que tenemos

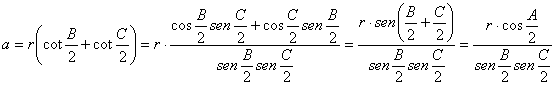
y, en consecuencia

■

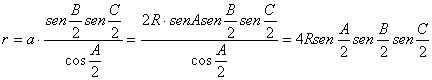Lema 2: “Sea ABC un triángulo acutángulo, O su circuncentro y D el punto de corte (distinto de A) de la bisectriz interior del ángulo A con la circunferencia circunscrita al mismo. Entonces ”.

Demostración: Obviamente el triángulo AOD es isósceles y teniendo en cuenta relaciones angulares elementales, tenemos que

con lo que llegamos a

■

Lema 3: “En todo triángulo ABC se cumple la identidad ”.

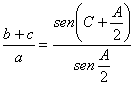Demostración: Basta con aplicar el teorema de los senos generalizado y recursos trigonométricos, puesto que

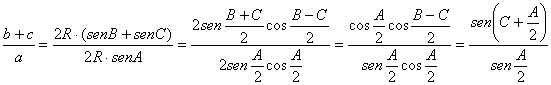
ya que claramente se tiene que . ■

Centrándonos ahora en nuestro problema, y aplicando los lemas 2 y 3, podemos observar que la longitud de la bisectriz interior prolongada AD, se puede expresar en la forma

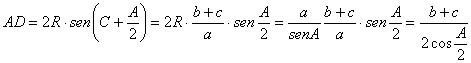[1]

Por otra parte, por potencia del punto O´ respecto de la circunferencia circunscrita al triángulo ABC, denotando por , S´ el punto diametralmente opuesto al punto S (respecto de la circunferencia circunscrita a ABC), y observando que O, O´ y S están alineados, podemos escribir que

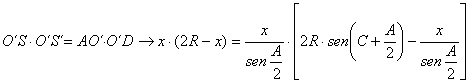
ya que Operando con la expresión anterior y empleando [1] llegamos a

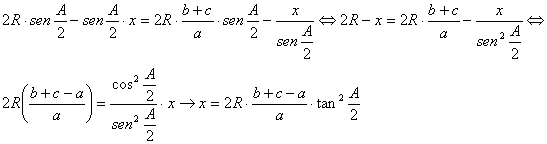
Finalmente, para demostrar que el punto M (punto medio del segmento PQ) del problema es el incentro del triángulo ABC, basta observar que dicho punto pertenece a la bisectriz interior que parte de A y además dista del circuncentro O precisamente la distancia que afirma el famoso teorema de Euler, es decir . Para ver esto, apliquemos el teorema de los cosenos al triángulo MOD, teniendo en cuenta que , , y . De esta forma, tenemos que , y además

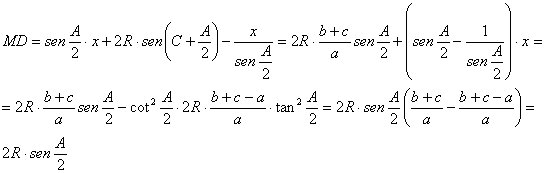
Así pues, tenemos que

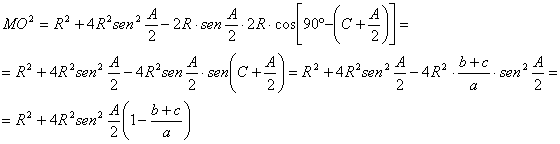
La proposición quedará demostrada entonces si demostramos la identidad

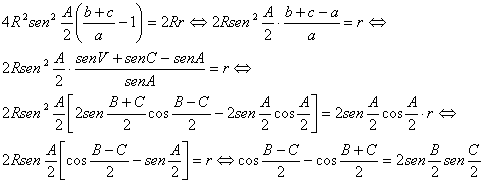
ya que

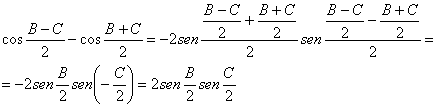
lo que demuestra la proposición.

---oooOooo---