Problema 523.- En un triángulo ABC, se construye un cuadrado con dos vértices sobre BC, un vértice sobre AB y otro sobre AC. Se definen de manera semejante los puntos , y , . Demostrar que las circunferencias circunscritas a los triángulos , y son mutuamente tangentes.

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Previamente demostraremos un lema que necesitaremos

Lema: “Sean los vértices de un cuadrado inscrito en un triángulo ABC de modo que el lado pertenezca al lado BC del mismo y al lado AB y al lado AC. Entonces el lado del cuadrado viene dado por

”.

Demostración: Descompongamos el área del triángulo ABC en el cuadrado , y los triángulos , y . Igualando áreas claramente tenemos que

■

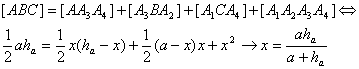Para demostrar que las circunferencias que circunscriben a los triángulos, y son mutuamente tangentes basta con demostrar que para cada dos de ellas, la distancia entre sus centros coincide con la suma de sus radios. Para ello, denotaremos por O el circuncentro del triángulo ABC y por , los circuncentros de los triángulos y , respectivamente.

Es claro también que el triángulo es homotético con el triángulo ABC, y con razón de homotecia k de valor (0<k<1) siguiente

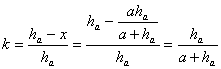
Emplearemos ahora el teorema de los cosenos en el triángulo y tendremos en cuenta que y además que

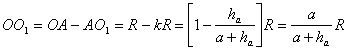
y análogamente para . De esta forma

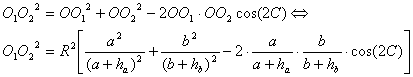
Por otra parte, utilizando el teorema de los senos generalizado y denotando por , los radios de las circunferencias que circunscriben a los triángulos y , respectivamente, tenemos que

con lo que tenemos

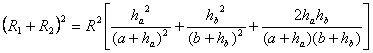
Por tanto, la proposición quedará demostrada si se cumple la identidad siguiente

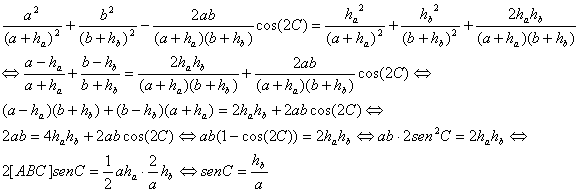
lo que demuestra la proposición.

---oooOooo---