Problema 524.- (Propuesto por Gennaro Rispoli, profesor de matemáticas en el Liceo Scientifico Sperimentale annesso al Liceo Gimnasio, Salerno, Italia)

Sea ABC un triángulo. Sea N el punto de contacto de la circunferencia inscrita con AC. Sea MN el diámetro perpendicular a AC en la circunferencia inscrita. Sea L la intersección de BM con AC. Demostrar que AN=LC.

Soifer, A. (2009) Mathematics as Problem Solving.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Previamente necesitamos dos lemas que demostramos a continuación:

Lema 1: “En todo triángulo ABC se tiene ”.

Demostración: Por consideraciones, recursos trigonométricos elementales, y empleando el teorema de los senos generalizado, es claro que tenemos

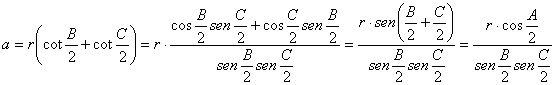
y, en consecuencia

■

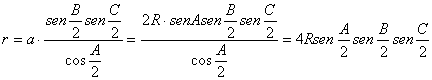Lema 2: “En todo triángulo ABC se tiene ”.

Demostración: Deduciremos una serie de relaciones relacionadas con los cosenos de los ángulos del triángulo ABC dado. Demostraremos la siguiente proposición auxiliar: “Con la notación habitual para un triángulo sea A un ángulo del mismo, entonces cosA es una raíz real de la ecuación polinómica siguiente:

”.

Para la demostración consideremos las relaciones (teorema de los senos generalizado) y (relacionada con el incentro). Tenemos, utilizando las identidades trigonométricas del ángulo doble

Elevando al cuadrado y operando se tiene que

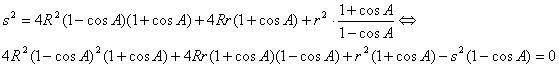
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes deducimos las relaciones

Finalmente, podemos determinar ya que

■

Centrándonos ahora en nuestro problema, tengamos en cuenta que la longitud AN es bien conocida y de valor . Sean , . Entonces, es claro que tenemos , y . En consecuencia, aplicando el teorema de los senos al triángulo BLC, tenemos

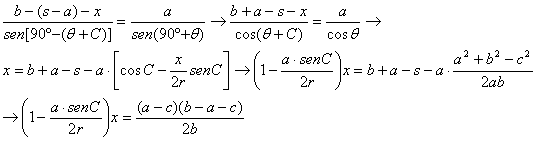
Por otra parte, teniendo en cuenta los lemas anteriores, relaciones trigonométricas elementales y el teorema de los senos generalizados, el primer paréntesis de la última igualdad se puede escribir en la forma

y, en consecuencia, como , podemos determinar el valor de NL

Finalmente, podemos determinar el valor de LC, de modo que

lo que concluye la demostración de la proposición.

---oooOooo---