Problema 525
Sea H el ortocentro del triángulo ABC. Demostrar que las circunferencias de diámetros CH y AB son ortogonales.
Alasia, C. (1900), La recente geometria del triangolo, problema 195, pag. 293
Solución: Gennaro Rispoli, profesor de matemáticas en el Liceo Scientifico Sperimentale annesso al Liceo Ginnasio "T.L. Caro", 84087 Sarno (Salerno), Italia
Costruzione geometrica
Dato il triangolo ABC, consideriamo:
· le rette AS, BR e CQ rispettivamente perpendicolari ai lati BC, CA e AB del triangolo di riferimento;
· l’ortocentro H del triangolo ABC;
· il punto medio M di AB e la circonferenza di centro M e raggio MB;
· il punto medio N di HC e la circonferenza di centro N e raggio NC.
Dette circonferenze si intersecano naturalmente nei punti R ed S. Le stesse circonferenze hanno inoltre RS come asse radicale ed NM come retta dei centri.
Consideriamo infine il punto medio K di NM e la circonferenza di centro K e raggio KM o KN.
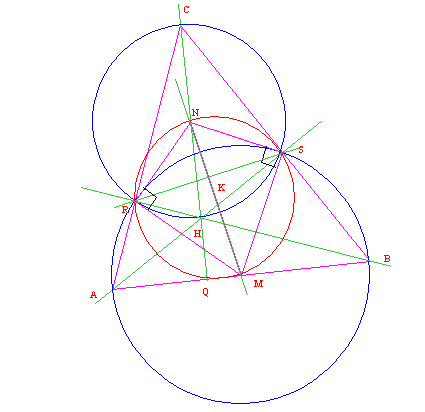
Dimostrazione
Si tratta di provare che le rette MS ed NS o RM ed RN sono rette perpendicolari.
Vediamo in primis che l’angolo ÐASC è retto sia perché AS svolge il ruolo di altezza del triangolo ABC relativa a BC sia perché il triangolo HSC è inscritto nella semicirconferenza di centro N e diametro HC, dove NS svolge il ruolo di raggio. Così l’angolo ÐBSA è retto.
L’asserzione si prova anche osservando che il triangolo BSA è inscritto nella semicirconferenza di centro M e diametro AB, dove MS svolge la funzione di raggio.
Abbiamo che la retta dei centri NM è asse del segmento RS ed i segmenti NS ed MS sono perpendicolari essendo il primo raggio della semicirconferenza di centro N e diametro HC ed il secondo tangente alla detta semicirconferenza nel punto S.
L’asserzione si prova anche osservando che MS è raggio della semicirconferenza di centro M e raggio MB ed NS è tangente alla detta semicirconferenza nel punto S.
Georg E. Martin, Geometric Constructions, Springer, New York, 1998 (Chapter 1, Euclidean Constructions, pag. 15)