Problema 525
Siga
H l’ortocentre del triangle 
. Demostreu que les circumferències de diàmetres 
i 
són ortogonals.
Alasia, C. (1900): La recente geometria del triangolo, problema 195, pag. 293
Solució de Ricard Peiró.
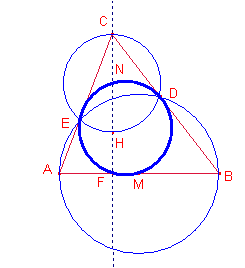
Dues circumferències són ortogonals si les tangents en els punts secants són perpendiculars.
A fi que dues circumferències siguen ortogonals el triangle que determinen els centres i cadascun dels punts de tall són triangles rectangles i l’angle recte el formen els punts d’intersecció de les circumferències.
1.- Solució geomètrica sense coordenades.
Siga
H l’ortocentre del triangle .
Siguen
AD, BE, CF les rectes altura del triangle .
La
circumferència de diàmetre té centre N, el punt
mig del segment .
, aleshores el punt D pertany a la circumferència.
Anàlogament E pertany a la circumferència.
La
circumferència de diàmetre té centre M, el punt
mig del segment .
, aleshores el punt D pertany a la circumferència.
Anàlogament E pertany a la circumferència.
La intersecció de les dues circumferències són els punts D, E.
Vegem que el quadrilàter FMDN és inscriptible en una circumferència.
és un angle central de
circumferència i abraça un arc 
.
és un angle central de
circumferència i abraça un arc de 
.
Notem
que els angles , són suplementaris,
aleshores el quadrilàter FMDN és inscriptible en una circumferència.
Per
tant els angles 
, 
són suplementaris.
Aleshores, 
Anàlogament FMEN és un quadrilàter inscriptible i raonant d’igual forma
.
Per tant, les circumferències són ortogonals.
2.- Demostració amb coordenades cartesianes.
Considerem
el triangle amb les següents
coordenades cartesianes:
, 
, 
.
El
centre de la circumferència de diàmetre és el punt mig del
segment. Les seues coordenades són: 
.
El
peu de l’altura sobre el costat té coordenades: 
. La recta altura sobre el costat té equació 
.
La
recta altura sobre el costat 
té equació 
.
La
intersecció de les rectes 
és l’ortocentre del
triangle que té coordenades:
.
El
centre N de la circumferència de diàmetre , és el punt mig del segment , té coordenades: 
.
El
radi de la circumferència de diàmetre és: 
.
El
radi de la circumferència de diàmetre és: 
.
, 
.
Aplicant
el teorema de Pitàgores al triangle rectangle 
:
.
.
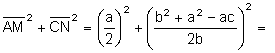
Aleshores, 
. Per tant les dues circumferències són ortogonals.