Problema 525
Sea H el ortocentro del triángulo 
. Demostrar que las circunferencias de diámetros 
i 
son ortogonales.
Alasia, C. (1900): La recente geometria del triangolo, problema 195, pag. 293
Solución de Ricard Peiró.
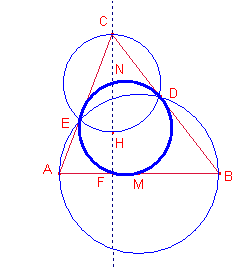
Dos circunferencias son ortogonales si las tangentes en los puntos secantes son perpendiculares.
Para que dos circunferencias sean ortogonales el triángulo que determinen los centros y cada uno de los puntos de corte son triángulos rectángulos y el ángulo recto lo forman los puntos de intersección de las circunferencias.
1.- Solución geométrica sin coordenadas.
Sea H el ortocentro del triángulo .
Sean AD, BE, CF las rectas altura del triángulo .
La circunferencia de diámetro té centro N, el punto
medio del segmento .
, entonces el punto D pertenece a la circunferencia.
Análogamente E pertenece a la circunferencia.
La circunferencia de diámetro tiene centro M, el punto
medio del segmento .
, entonces el punto D pertenece a la circunferencia.
Análogamente E pertenece a la circunferencia.
La intersección de las dos circunferencias son los puntos D, E.
Veamos que el cuadrilátero FMDN es inscribible en una circunferencia.
es un ángulo central de circunferencia y abarca un arco 
.
es un ángulo central de circunferencia y abarca un arco de 
.
Notemos que los ángulos , son suplementarios, entonces
el cuadrilátero FMDN es inscribible en una circunferencia.
Por tanto los ángulos 
, 
son suplementarios.
Entonces, 
Análogamente FMEN es un cuadrilátero inscribible y razonando de igual forma
.
Por tanto, las circunferencias son ortogonales.
2.- Demostración con coordenadas cartesianas.
Consideremos el triángulo con las siguientes coordenadas
cartesianas:
, 
, 
.
El centro de la circunferencia de diámetro es el punto medio del segmento.
Sus coordenadas son: 
.
El pie de la altura sobre el lado té coordenadas: 
. La recta altura sobre el lado tiene ecuación 
.
La recta altura sobre el lado 
tiene ecuación 
.
La intersección de las rectas 
es el ortocentro del triángulo que tiene coordenadas:
.
El centro N de la circunferencia de diámetro , es el punto medio del segmento , tiene coordenadas: 
.
El radio de la circunferencia de diámetro es: 
.
El radio de la circunferencia de diámetro es: 
.
, 
.
Aplicando el teorema de Pitágoras al triángulo rectángulo 
:
.
.
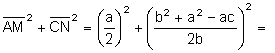
Entonces, 
. Por tanto las dos circunferencias son ortogonales.